The question is: "What is an equation, and what is an expression?" The New Zealand curriculum has Equations and expressions as one of the four subsections of Number and Algebra, but doesn't say what each of these are. This article is here to help. It also gives more information about equations, and information about the different ways letters are used in algebra (e.g., x, y, a, etc.). These letters are called pronumerals.
Expressions
An expression is a combination of symbols that follow correct mathematical conventions. The symbols are most often numbers (e.g., 3 , 4.2 etc.), pronumerals (i.e., letters that stand for numbers, e.g., x, y, z etc.) or operations (e.g., +, –, ×, ÷, etc.)
Types of expressions
- Number expressions A mix of numbers and operators, e.g., 7; 3 + 4; 16 × 8 + 32; 3(4 + 5) ÷ 2
- Algebraic expressions A mix of numbers, operators, and pronumerals, e.g., x + 3; x2 + 2x + 1; (a + b) / 2
Number expressions can be evaluated using the rules of arithmetic to get a numerical answer (e.g., the expression 3 + 4 is the same as 7)
Algebraic expressions cannot be evaluated in this way. This lack of a single number solution is referred to as "lack of closure", and can be a stumbling block to students. For example, 2x + 6 has no specific numerical value. We can, however, come up with equivalent expressions, e.g., 2(x + 3) = 2x + 6.
Expressions and terms
Expressions can be thought of as being composed of terms. A term is a series of numbers and operators that are linked multipicatively. For example: 3x2; 2x; 5x; or 6xy. Terms with the same combination of pronumerals are called like terms. For example 2x and 5x are like terms. Like terms can be added, so 2x + 5x = 7x and 3xy + 4xy = 7xy.
This diagram gives the names of different parts of an expression:
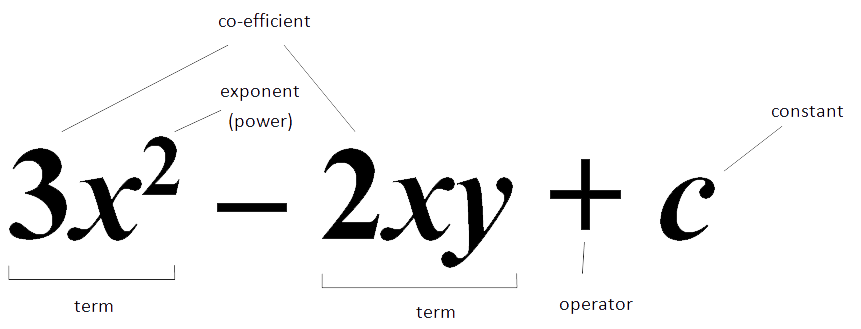
Equations
An equation is a statement about whether two mathematical expressions are equal. By "equal" we mean that the value of each side is the same. So 3 × 4 = 4 × 3, even though they represent different situations (i.e., 3 lots of 4 and 4 lots of 3 respectively).
Types of equations:
- Number equations These are generally written as true statements, e.g., 3 + 4 = 7 6 × 8 = 8 × 6 3(4 + 5) = 27
- Algebraic equations The truth of these statements depends on the values of the pronumerals. e.g., x + 3 = 7 y = x2 E = mc2
In primary school we are usually dealing with number equations. We often refer to these as number sentences.
In secondary school (as well as sometimes at intermediate school), algebraic equations become the focus. At this level, it becomes important to discuss the different ways that pronumerals (x, y, E, m, c etc.) are used.
An analogy with natural language
Equations can be thought of as sentences, while expressions can be thought of as phrases.
In natural language, a sentence must have a verb. In mathematical sentences, i.e., equations, the verb is "=".
Two approaches to equations
There are two ways of thinking about equations.
1. Equations as a "balance" or "it has the same value as" statement
This means that the amount on each side of the equals sign is the same.
| Number equations | 3 + 4 = 7 | 50 = 60 – 10 | 6 × 8 = 8 × 6 | 3(4 + 5) = 27 |
| Algebraic equations | x + 3 = 7 |
2(x +1) = 2x + 2
|
y= x2
|
E = mc2
|
| This means x = 4 |
x can be any value
|
For every value of x, there is a corresponding value of y.
(e.g., if x = 3 then y = 9)
|
For every value of m, there is a corresponding value of E. |
2. Equations as true or false statements
This approach is particularly useful at a secondary school level with algebraic equations.
This approach is particularly useful at a secondary school level with algebraic equations.
It is also useful at a primary level to discuss whether number equations are true or false. See Algebraic thinking concept map.
It is also useful for computer programming.
|
Number equations True equations False equations |
3 + 4 = 7 3 + 4 = 6 |
50 = 60 – 10 | 6 × 8 = 8 × 6 | 3(4 + 5) = 27 |
| Algebraic equations | x + 3 = 7 |
2(x +1) = 2x + 2
|
y= x2
|
x2 + 1 = 0
|
| True if and only if x = 4 |
True for all values of x
|
For every value of x, there is one value of y that makes the equation true.
( eg., if x = 3 then y = 9) |
There are no values of x which make this statement true. (i.e., for no real numbers –but there are complex numbers, such as √–1, which can make this statement true) |
Some equations may have two or more values that make it true, e.g., (x – 2)(x – 3) is true if x = 2 or x = 3.
Pronumerals
These are letters which represent a number or a range of numbers. In more advanced mathematics, they may represent an object, such as a vector or a matrix. Pronumerals are often referred to as variables. This, however, obscures the different roles that pronumerals take. We will break pronumerals down into four different classes, each playing a somewhat different role.
Pronumeral as the unknown
This is when there is an equation which has to be solved.
For example: x + 3 = 7 This can be read as : "Find a value (or values) of x so that x + 3 = 7 is a true statement".
This is only true if x = 4. It is false for all other values of x.
For example: x + 3 = 7 This can be read as : "Find a value (or values) of x so that x + 3 = 7 is a true statement".
This is only true if x = 4. It is false for all other values of x.
Pronumeral as a variable
This is when the value of the pronumeral changes with respect to another.
This is when the value of the pronumeral changes with respect to another.
For example: y = 2x This can be read as : Find the corresponding value of y that will make the equation true for different values of x.
This means that the values of y vary, as x varies (and hence the term "variable"). So, if x = 2 then y = 4 makes the equation true, and if x = –1/2 then y = ⁻1 also makes the equation true.
All the possible values of x that are used are called the domain of the function, and the values of y are called the range. These relationships can easily be graphed.
This means that the values of y vary, as x varies (and hence the term "variable"). So, if x = 2 then y = 4 makes the equation true, and if x = –1/2 then y = ⁻1 also makes the equation true.
All the possible values of x that are used are called the domain of the function, and the values of y are called the range. These relationships can easily be graphed.
Pronumeral as a constant
This is where the pronumeral stands for a fixed numerical value.
For example in Einstein's famous equation E = mc2,
This is where the pronumeral stands for a fixed numerical value.
For example in Einstein's famous equation E = mc2,
where c stands for the speed of light = 300,000 metre per second, but E and m are variables.
Pronumeral as a parameter
This is where the pronumeral stands for a quantity (most often a number) which describes different members of a family (or system) of related equations.
For example: y = mx
This is where the pronumeral stands for a quantity (most often a number) which describes different members of a family (or system) of related equations.
For example: y = mx
This describes all the different possible straight lines which go through the origin, but have different slopes. The parameter is m. The slope of the line changes as m changes, e.g., y = 4x is steeper than y = 2x.

