Balancing see-saws

Balancing see-saws

Pencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about levers and forces.
Adults and small children can have a successful see-saw if they sit in the right place.
"OH DEAR" "YES, IT WORKS"
Tui and Sonny decided to model the see-saw using a ruler and 50 g masses.
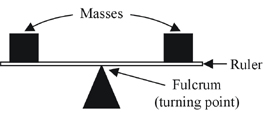
They put different number of masses on each side and moved them until the ruler was balanced. Then they recorded the mass and its distance from the turning point (fulcrum) for each side.
Here are their results:
Left-hand side
Right-hand side
mass (g)
distance from fulcrum (cm)
mass (g)
distance from fulcrum (cm)
50
100
150
200
8
6
5
4
100
150
50
100
4
4
15
8

Question 1Change answer

a) Tui said, "I can see a rule for this. Multiply mass × distance for the left-hand side; it equals mass × distance for the right-hand side." Use evidence from the table to show that Tui is right. 

Question 1Change answer

b)  If 400 g is placed 10 cm from the fulcrum, how far from the fulcrum must 100 g be placed for the ruler to be balanced? (Show your working.) 

Question 1Change answer

c) Tui's mother weighs 60 kg. She sits 0.4 m from the fulcrum. Tui's young sister weighs 12 kg. Where must his sister sit for them to have a successful see-saw? (Show your working.)
Task administration: 
This task can be completed with pencil and paper or online.
Level:
5
Curriculum info: 
Science, Communicating in science, Physical World
Keywords: 
physical inquiry, forces, levers, balance, formulae
Description of task: 
Task: interpret data from a table and complete two calculations. The context is balancing a see-saw. Assessment focus: using a scientific formula to identify trends.
Curriculum Links: 
Science capabilities
The capabilities focus is brought about by the conversations you have and the questions you ask.
 
Capability: Interpret representations
This resource provides opportunities to discuss the use of scientific formulae to predict relationships.
 
Science capabilities: 
Interpret representations
Answers/responses: 
  Y10 (11/2003)
a) For more than 1 of the four accurate examples, e.g.,
50 g × 8 cm = 400 (left-hand side) equals 100 g × 4 cm = 400 (right-hand side), etc., or
For any 1 of the four accurate examples, or
Attempt made at showing the relationship.
difficult
 
easy
easy
b) For showing working, e.g.,

400 × 10 = x × 100, or
4000 = 100x

For correct answer, x = 40
For correct unit, i.e., answer = 40 cm.
moderate
 
 
moderate
easy
c) For showing working, e.g.,

60 × 0.4 = 12 × x or
24 = 12x

For correct answer, e.g., x = 2
For correct unit, i.e., answer = 2 m.
moderate
 
 
moderate
moderate
Diagnostic and formative information: 

A number of students did not appear to understand what would constitute evidence of the mathematical relationship described. They either left part a) blank or wrote wild guesses. Others were content to give just one example and very few gave all four of the examples available to them. Students could benefit from a range of opportunities to explore the nature of evidence – even when that seems very obvious. The question of whether one example or more should be given could lead to a discussion of the sufficiency of evidence.