Jonathan Fisher (2010)
Dividing one fraction by another fraction can be a difficult maths problem to conceptualise, represent, or solve with understanding.
In mathematics division can be defined as the inverse of multiplication:
c × b = a, a⁄b = c (a ÷ b = c), or dividend⁄divisor = quotient
The division operation can take two forms: partitive division and quotitive division:
Partitive division (partition) involves sharing a quantity (dividend) between a given number (divisor) of equal-sized groups. For example the question 72 ÷ 8 could be read as 72 shared between 8 groups. Fraction division problems can be especially difficult to conceptualise using the partitive division: The problem, 2/3 ÷ 1/3, would be phrased 2/3 shared amongst 1/3. This is not easy to explain or give a real life example of.
Quotitive division (quotition) involves finding how many groups of a given size (divisor) will go into a given quantity (dividend).
For example the question 72 ÷ 8 could be read as how many groups of 8 go into 72?
Applying the quotitive lens to fraction problems can help to visualise, represent and conceptualise (and ultimately solve with understanding about the number properties involved).
The problem: 2/3 ÷ 1/3, would be phrased How many 1/3s in 2/3?.
Quotitive division can involve holding the 1/3 as a reference unit and interpreting the 2/3 in terms of another unit (called unitising). This solution is immediately obvious and simple (in this case). Interpreting fraction division problems as quotitive division work for problems where the quotient is greater than (the dividend is greater than the divisor) or less than one (the dividend is less than the divisor). The latter is more common in division problems and tends to be easier to conceptualise or represent.
An example where the quotient is greater than one is 4/5 ÷ 2/5. Using quotitive lens this could be asked how many 2/5 in 4/5?
Answer: There are two 2/5s in 4/5.
An example where the quotient is less than one is 2/5 ÷ 4/5.
Using quotitive lens this could be asked how many 4/5 in 2/5?
Answer: There is half of a 4/5 in 2/5.
Using the multiplicative inverse (understanding or procedure?)
For solving division problems with fractions many students have learnt that they can swap the denominator and numerator of one of the fractions (not always the correct one) and multiply (not necessarily knowing why). The rationale behind this is that multiplication and division have an inverse relationship (a Year 8 National standard) and multiplying by the inverse is the same as dividing by the number (i.e., a ÷ b = a × 1/b or a lots of 1/b). This relates to the definition of division shown above.
For example, 5/7 ÷ 2/3 becomes 5/7 × 3/2 (inverted divisor) which can be solved using basic facts and a basic understanding of writing fractional notation. As a result this strategy could be a learned procedure rather than reflecting students understanding of multiplicative inverse. Students still need to be asked why they "swapped" the fraction.
Other strategies to solve fraction division problems
Some students can solve the problem by dividing the two fractions but maintaining the correct relationships (i.e., correctly handling the multiple layers of division operations).
Students could also use a part-whole strategy and recognise the relationship between the two fractions to show (using substitution):
2/3 ÷ 1/3 → 2/3⁄1/3→ 2 × 1/3⁄1 × 1/3 →2 × a⁄1 × a [a = 1/3] → 2a⁄a = 2⁄1 [because 1/3 ÷ 1/3 = 1]
Students may recognise that 2/3⁄1/3 is the same as 2/1 because the 2/3 is twice 1/3 (or if 1/3 = a, then the problem could be seen as 2a/a, which is 2). This works because both have a common denominator. These calculations can be difficult and reasoning becomes more difficult when the numbers are less related (i.e., denominators not being multiples or having common factors, e.g., 2/7 ÷ 5/9). In this case common denominators could be identified and then the above strategy be used. Although finding common denominators for fraction division problem can be seen as superfluous, it can be a very useful strategy to explore the meaning of the division and support student understanding of the problem.
Students could also represent the problem with a diagram or drawing. For example, they could solve 3/4 ÷ 1/2, using a quotitive lens. This could involve drawing a 3/4 shape and then looking at how many 1/2s would fit into it:
If is 
3/4 and 
is 1/2.
How many fit into ?
Solution: 
[one and a half].
Another way to represent the problem is as an area diagram. For these problems, note the relationship with the common denominator, i.e., 3/4 ÷ 2/4 (or 2/4 ÷ 3/4).
For example, the problem 3/4 ÷ 1/2 could be first drawn as 3/4.
After this 1/2 could be circled, and the question asked how many of these (circled part) fit into the shaded shape?
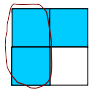→ one half and a half (of a half) left.
For the problem 1/2 ÷ 3/4, 1/2 could be shaded first,
3/4 circled and the question asked how many of these (circled parts) fit into the shaded shape?
→ it look like two parts of three, which is 2/3
It is important to note that students' ability to use a range of strategies to solve fraction (and mathematics) problems can support more transferrable and flexible mathematical problem solving. Accordingly, using a quotitive lens should be one of many strategies that students explore to solve fraction division problems. Ultimately if students can explore different ways to solve the problem with understanding then they are more likely to correctly apply their strategy for solving the problem.