How many fractions?
| a) | Show how to work out how many 14's in 3. | |
|
||
| b) | Show how to work out how many 16's in 23. | |
|
||
| c) | Show how to work out how many 12's in 34. | |
|
| d) | Show how to work out how many 13's in 16. | |
|
- Using incorrect derivations of Invert and multiply, cross multiplication, unitising or uses a diagram that does not represent the fraction involved.
- Using Invert and multiply, cross multiplication, unitising, or sufficient diagrams, but not correctly to solve questions a)-b).
- Using Invert and multiply, cross multiplication, unitising, or sufficient diagrams to correctly solve questions a), and b) but no evidence of understanding.
- Using multiplicative strategies such as equivalence or division and cancelling out (using multiplicative identity) to correctly solve questions a)-c), indicating flexible use of the strategies.
| Y8 (10/2010) | ||
| a) |
12 Accept 12/4 [partial credit] as it is very close to the correct answer. Working that involves any of the following:
|
moderate moderate moderate |
| b) |
4 Accept 4/6 or 2/3 [partial credit] as they are very close to the correct answer. Working that involves any of the following:
|
difficult moderate moderate |
| c) |
11/2 or 3/2 or 6/4 Accept 1 remainder 2, 11/4, or half and a quarter 5 [partial credit] Working that involves any of the following: 
|
difficult difficult moderate |
| d) |
1/2 4 Working that involves any of the following:
|
very difficult difficult |
Based on a representative sample of 191 students.
NOTES:
- Students who solved the problem using invert and multiply or a form of cross multiplication need to be asked why they thought they could do this to solve the problem - simply using a memorised process does not constitute understanding.
- Other named strategies may involve elements of equivalence.
- Strategies that are based on correct premises and could lead to a correct solution.
- A significant number of students noted that 1/3 does not go into 1/6 therefore answered zero.
- For question c) students may identify that there is a half and something else (a quarter) or give a whole number solution as there is only one 1/2 in 3/4 . These students should be asked if there is anything left over (see next steps).
This resource is about being able to work out multiplicative relationships between fractions. The situation of how many x's in y is known as the quotitive approach of division (as opposed to partitive division, see Division with Fractions article). These division problems can take the form of reverse multiplication problems.
Prior knowledge
In order to solve these questions students should know something of the nature of fractions (the part-whole relationship between the numerator and denominator) and that they are numbers and as such have a size and can be operated upon.
Students used a variety of strategies to solve these problems; many of which involved diagrams. There were some very simple diagrams that could be used to show the relationship between the two fractions (side by side or overlaid). There were also a notable number of diagrams that were not sufficiently used to support an argument or illustration of how to get the answer. Other students used equivalent fractions to get common denominators or found a unit fraction and incremented up to find how many times it went into the divisor (unitising).
See Student work samples [pdf] for examples of the different student strategies.
| Common response | Likely misconception | |
| d) | 2 (inverse: 1/6 in 1/3) |
Whole number interpretation of fractions Students indicate that there are two 1/3's in 1/6's because there are two 3's in 6. |
|
a) b)
|
3 and working  6 and working 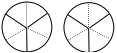 |
Diagrams are icons not representations of fractions Students draw a diagram that represents both fractions but do not correctly interpret it, e.g., for question a), each shaded circle represents a quarter, there are 3 circles and there are 3 quarters, therefore, the answer is 3. For b) the diagram of two circles cut into thirds shows 2/3 and then students work out how many sixths in those (2 circles) by drawing lines to make sixths (dotted). |
|
a) b) |
12/4 (3/1 x 4/4) 4/6 (2/3 x 2/2) [partial credit] |
Calculation and then conceptual misrepresentation Students calculate the solution of 1/4 into 3/1 by multiplying to get a common factor, e.g., multiplying 3/1 by × 4/4 → 12/4 . Some students multiplied 1/4 × 4/4 × 1/1 . These are both misapplications of multiplying by the identity. Essentially this misconception relates to a calculation error, but students have an answer very close to a fully correct answer (12/4 as opposed to 12 quarters). They are out by a factor that stems from their calculation using the multiplicative identity. |
|
a) b) c) d) |
4 (2/3 x 2/2 = 4/6) 2 (3/1 x 4/4 = 12/4) 2 (1/2 x 2/2 = 2/4) 2 (1/3 x 2/2 = 2/6) |
Equivalence calculation error While students try to develop equivalent fractions to compare they make miscalculations, e.g., for question b) students may know that sixths are smaller than thirds, but have difficulty getting equivalent fractions to work with, e.g., 2/3 × 2 = 4/6 so 2 is the factor (rather than multiplying by 2/2 and realising it is an equivalent number), or they identify the relationship between the parts of 1/6 and 2/3 as 2 [both numerators and denominators relate by a factor of 2]. |
|
c)
d) |
1
0 [partial credit] |
Factors must be whole number (division must be by the smaller number) Students identify that there is just 1 complete half in 3/4, but do not recognise or consider that remaining part. Students note that because 1/3 is greater than 1/6 it cannot "go into it". |
| d) | 2 (inverse: 1/6 in 1/3) |
Swap the order of fractions (won't go error) Students swap the fractions around to divide (can't divide 1/3 by 1/6 because it is smaller). This is like the "won't go"6 subtraction error |
| c) |
1/2 + 1/4 [partial credit] |
Cannot combine fractions to write as a complete fraction Students identify that there is one complete half in 3/4 (1/2 + 1/4 = 3/4), but cannot give the remainder (of 1/4) as a relative part of the divisor (i.e., 1/4 ÷ 1/2). |
NOTE:
6. The "won't go" error in subtraction involves students swapping the order of a subtraction equation if the subtrahend is larger than the minuend (i.e., for c - b = a; if b is larger than c, then b and c are swapped and the equation solved becomes b - c = a).
Whole number interpretation of fractions
Students who exhibit whole number misconceptions about fractions may need to explore the relationship between the numerator and denominator, and how this describes the size of the fraction. Resources that compare fractions [Ordering filled bottles, Larger fractions II, Close to a half] and use number lines to order fractions [Fraction long jump] can support this learning about fractions as numbers. Getting students to draw and label diagrams can also help to conceptualise the fraction problem.
Insufficient diagrams
For students who attempted to use diagrams to show how they solved the problems, ask them to label and explain how the diagrams worked. The diagrams should be comparable, i.e., of the same whole/size so that the size of the parts can be compared and discussed. Ensure that students do not change the referent whole7
as they make their explanations (e.g., 1/3 of one circle can look the same as 1/6 of two circles. The resources Sharing shapes, Partitioning pizza & fruit loaf, and Sharing cake and pizza explore this idea of maintaining the same whole when partitioning and naming fractions. For further information about partitioning see the Fractional thinking concept map: partitioning.
Get students to think about or even write their explanation for somebody else who is trying to understand how their strategy works. Some of the misconceptions with these questions related to students only having experienced fractions as shaded diagrams and they may lack the experience of creating their own partitions to develop the representation of the fraction, i.e., they think that the diagram is the fraction; rather than one of the many representations of the fraction. As well as exploring the idea of partitioning (see resources above), these students could be asked to draw a number of different diagrams to present one fraction (for example three-quarters).
Calculation and then conceptual misrepresentation or equivalence calculation error
Before embarking on solving these problems students could be asked to describe in their own words what that question is asking them to do. They could also be asked how they can find out what "goes into" means (what operation?) and whether they can give a whole number example (this would be a great indicator that they understand the operational nature of the problem). Students could also explore the idea of "goes into" with whole numbers (e.g., how many 4s in 20? then possibly how many 10s in 5?) and how they solve it. Then ask how many halves in 1? And how many 1s in a half?
Once they have developed an understanding of this as a division exercise, they could look at how they are working out the equivalent fractions. Many of these students multiplied the fractions by a fractional form of the multiplicative identity (e.g., 4/4 , 2/2 , or a/a). It is a very common misconception that a/a is somehow a (when it comes to multiplying) and somehow not a when it comes to why the numbers are being multiplied. Students need to be asked why they multiply by a/a. They should be able to justify its use (multiplying by one and any fraction a/a = 1, and how they can use this to rename the fraction). For the purposes of this resource the focus is on drawing on the range of students' strategies they use to solve to develop their understanding. Students who use this method of equivalence could also be asked to illustrate their thinking about what they are doing in parallel to their working. Drawing diagrams of this may support their thinking.
NOTE:
7. If the referent whole (the whole being referred to) of these diagrams is the same size, then the size of the parts can be also visually compared. Otherwise it would not be visually workable as it would be pointless to visually compare 1/4 of one shape with 1/3 of another - it would mean nothing.
Factors must be whole number (divisor must be smaller) or Swap the order of fractions
These students may be using fractions to work with but not thinking about what it means when they have fractional answers in this context. Asking a question like "How many 1s in a half?" may not make sense (because "you can't have a one in a half), so possibly re-wording to "How much of one is in a half?" may lead them into recognising that there is a half of 1 and therefore that a part of a larger number can be in a smaller number (answers can be rational numbers). Again using diagrams to develop understanding can help, but students should be starting to express these situations in number form. This misconception relates to thinking in terms of whole numbers rather than rational numbers, and is very common as we tend to work predominantly in whole numbers.
Cannot combine fractions to write as a complete fraction
These students have identified that there are portions of larger numbers in smaller numbers, but cannot describe them as single fractions. For example, question c) how many halves in threequarters? First of all there is 1 (or there is a "half") but there is also some other bit left (1/4). These students are conceptually correct and indicate the understanding about the meaning of these fraction problems. The key here is to think in terms of the divisor (what is being divided into): for question c) the division expression would be 1/2 × ? = 3/4 (quotitive division) or 3/4 ÷ 1/2 = ? (partitive division). Click on the link to see the Division with Fractions article. The divisor is half, so the answer should be given in terms of half (how many halves). Students gave their answer 1/2 + 1/4 ; so they have identified that there is 1 half and 1/4 (i.e., 1 half with a quarter left over). It is important to keep the half in mind for identifying the other part, calling it a quarter refers to a quarter (generally) not a quarter in relation to a half (a quarter being half of half). It is maintaining the answer in reference to the divisor that keeps the integrity of numbers they are working with. This common reference is very similar to the idea of referent whole.
Sufficient diagrams
The use of diagrams can aid students in the conceptual understanding of the problem rather than learning a process for solving without understanding (e.g., invert and multiply). However, ultimately students should be moving towards using the fractions as numbers to solve these types of fraction problems. Get students to label their diagrams and then write their explanation for somebody else who is trying to understand how their strategy works.
Successful strategies
Students who used successful strategies such as Invert and multiply, cross multiplication, unitising, to work out how many of each fraction in the other could be asked if they could use another strategy to solve the problem. Being able to use a range of multiplicative strategies is an indicator that students may be at Stage 7 (Advanced Multiplicative) as opposed to Stage 6 (Early Multiplicative) of the Number Framework.
Whole class discussion
Many of the above next steps can be explored in Mathematical classroom discourse where students share and critique their own and others' strategies to develop a fuller understanding.
For further information about partitioning see the Fractional thinking concept map: partitioning.