Dividing fractions
|
Do NOT use a calculator for this task.
|
||
| a) | Show how to solve 4 ÷ 45 | |
|
||
|
b)
|
Show how to solve 23 ÷ 6.
|
|
|
|
c)
|
Show how to solve 34 ÷ 17
|
|
|
|
d)
|
Show how to solve 85 ÷ 23
|
|
|
|
e)
|
Show how to solve 2512 ÷ 456
|
|
|
Links to the Number Framework
The strategies that students use can help determine their stage of development within the Number Framework. Strategies that could be used for this resource include visual representation, exploring the quotitive relationship in division, recognising the inverse relationship of multiplication and division and using that to turn the problem into a multiplication problem. Students using a range of multiplicative strategies with whole numbers are indicating Stage 7/Level 4 (Advanced multiplicative), but this resource can involve working with the multiplicative inverse as well as dividing with fractions (and mixed fractions). This addresses a range of multiplicative strategies and maintaining order of operations which is more like stage 8 (Advanced Proportional).
| Y10 (11/2009) | ||
| a) |
5 or 20/4 [accept 5/1] and working involving:
|
difficult difficult |
| b) |
1/9 or 2/18 And working involving strategies as above. |
difficult |
| c) |
21/4 or 5 1/4 |
difficult |
| d) |
12/5 or 24/10 or 2 2/5 or 2 4/10 |
difficult |
| e) |
1/2 |
difficult |
Strategies that involve students' converting to decimals and solving without a calculator are correct, but not the intended assessment focus for this resource (see Next steps).
Prior knowledge
An understanding that fractions are numbers, that they have a value (and size) and can be operated upon (addition, subtraction, multiplication, division, etc) is required. Students should have explored addition and subtraction before looking at multiplication and division.
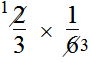
Other students inverted either side of the expression and made a calculation error–either with the order of operation or an operational error (e.g., added instead of multiplied).
Essentially the main errors were:
- Students cannot write given whole numbers as fractions (e.g., 4 and 6 become 4/4 and 6/6 ).
- Students have learnt a process without understanding and invert the wrong fraction (dividend instead of the divisor).
Question e) is a more difficult question as it requires students to work with two mixed fractions.
Students can either:
- convert these to improper fractions, invert the divisor, and then multiply larger numbers, or
- recognise the relationship between the parts of the two mixed fractions (2 is half of 4 and 5/12 is half of 5/6 ) and understand the part whole nature of whole numbers and fraction numbers in a multiplicative way (if 2 is half of 4 and 5/12 is half of 5/6 , then 2 5/12 is half of 4 5/6 ).
| Common error | Likely misconception | |
|
a)
b)
|
1 1/4
18/12 or 3/2 or 1 1/2
|
Students who cross multiply incorrectly or make a calculation error (including incorrect operator)
Students use 4/4 as 4, e.g., 4 ÷ 4/5 → 4/4 × 5/4 .
Students invert the dividend (LHS) and treat x = x/x , e.g., 6 = 6/6 .
|
|
a)
b)
c)
d)
e)
|
4/20 or 1/5
9/1 or 9
4/21
5/12
2/1 or 2
|
Solution is inverse of correct solution This misconception involved inverting the dividend (LHS) instead of the divisor (RHS) or some other incorrect form of cross multiplying, e.g., for question c) 3/4 ÷ 1/7 becomes 4/3 × 1/7 = 4/21 .
|
They may not be aware of why it is important to show their work. They may not have been required to do so in the past, or they may not know where to start. These students could be given examples of the question and peoples' strategies (correct and incorrect) and asked to use the strategy to work through the problem to derive the answer. Having students identify or write their strategies down reveals their understanding or misconceptions and can be analysed to work out next steps.
Students who cross multiply incorrectly or make a calculation error (including incorrect operator)
Students could check what they are multiplying and dividing. If they are also inverting the divisor they should be asked why they did so, and to explain their strategy. Knowing that they can invert the divisor is a piece of knowledge that could hinder students from understanding what they are actually doing and why they can do that. The inverse relationship between multiplication and division could be modelled first with whole numbers so students develop that understanding before applying a procedure without understanding it. Students could also be asked to solve simpler fraction division problems using different strategies/methods.
Incorrect fraction notation
Students who write a whole number as a fraction incorrectly, e.g., 4 as 4/4 may need to explore representing part-whole fractions to address this misconception. They could explore basic number lines showing 2/4 and 3/4 and ask what 4/4 would look like, and whether it is a whole (i.e., it is one). They could then explore other fractional amounts (e.g., 5/4 and count up to make 16/4 ). This understanding is a part-whole understanding of a fraction. Students also need to see that a fraction is a number with an abstract unit of one. They should have experienced adding and subtracting fractions as numbers before dividing or multiplying them. The three resources: Eating fractions of pie, pizza and cake, Eating fractions of cake; and Fractions and food are resources that look at adding and subtracting fractions as numbers (at levels 3, 4, 5 respectively).
Solution is inverse of correct solution
For students who solved the problem by inverting the LHS rather than the RHS, this is the danger of learning a procedure without understanding why. These students need to explore the relationship between multiplication and division and the concept of multiplicative inverse.
Note: the danger of using a set procedure without understanding why it can be used can mean that students learn "rules" rather than "concepts" (which tend not to support transferring learning to other similar concepts). This is especially true for division of fractions, where using a rule can provide students with a quick and simple method to solve division problems, but they miss out on the opportunity to find out for themselves. For example they may not find out about:
- another aspect of division (quotition),
- the inverse relationship between multiplication and division, or
- the rules for working with multiplication and division with fractions (rationale numbers) which are similar to working with whole numbers (relating to the fact that one fraction can be a quotient relationship between two numbers).
Students who convert the fraction to decimals and solve.
Although, this strategy may yield a correct answer, the intended assessment focus for this resource is working with the division relationship of fractions. Students could be asked if they can work out the answer without using a decimal value of the fractions. They could either explore the quotitive aspect of division (see Division with fractions) or the inverse relationship of multiplication and division.
Students who divide the numerator and denominator separately
Dividing the numerator and denominator is a correct and workable method when the denominators are the same. Otherwise the calculation requires very careful attention to detail, e.g., 8/5 ÷ 2/3 can become (8/2)/(5/3) = 4/(5/3) which is almost an equally hard division problem unless students are aware of the inverse nature of division and multiplication to get from 4/(5/3) to 4 × 3/5 (12/5). Students could be introduced to the quotitive aspect of division, see Division with fractions which looks at using a quotitive division model, or explore the inverse relationship of multiplication and division.
Students who find the common denominator and solve
Some students think they have to find a common denominator before to be able to solve this problem. Finding the common denominator is an unnecessary part of solving this division problem, and is generally only useful when solving addition and division fraction problems. In fact although finding the common denominator can help with dividing the numerator and denominator separately, it is a more difficult calculation than inverting and multiplying, and even looking at the problem from a quotitive division view. Ask these students why they found the common denominator.
Get them to solve some more simple fraction division problems (with and without common denominators: 2/3 ÷ 1/3 , 1/5 ÷ 3/5 ), and ask them if they need to find a common denominator and how it helps them to solve the problem. Encourage them to look at the fractions as numbers and find the relationship between them. For example 1/5 ÷ 3/5 can involve recognising that the divisor is 3 times larger than the dividend, so the solution is a third, or 2/3 ÷ 1/3 the divisor is half the size of the dividend, so the solution is 2. The inverse relationships can become apparent with these simple fraction numbers and can be explored using larger fractions before focussing on the invert and multiply strategy for solving division.
Exploring fraction using quotitive division model
Students can draw or represent the fractions division problem to work out what it is they are actually solving. Getting students to explain what they need to work out without actually starting any calculations should help them clarify the problem. Then they could check their findings using a diagram. For example 3/4 ÷ 1/2 could be investigated:
- Students could picture 3/4 of a cake and work out how many (and what fraction) people would get half a tray (1 person and half left over).
-
Students could also draw the 3/4 and then look at how many 1/2s would fit into the shape,
e.g., is 3/4 and
is 3/4 and  is 1/2 .
is 1/2 .
How many _____________ fit into _______________ ? (one and a half).
This idea of "how many xs fit into y (or how many 1/2s in 3/4) is the essence of quotitive division.
Multiple strategies are an important part of an Advanced Multiplicative stage of The Number Framework, and students should be able to indicate a range of strategies and discuss more efficient methods.
Click on the link for more information about quotitive division with fractions.

