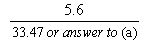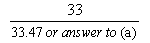Kicking for goal

Kicking for goal

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Further Resources
This task is about using trigonometry to find missing lengths.
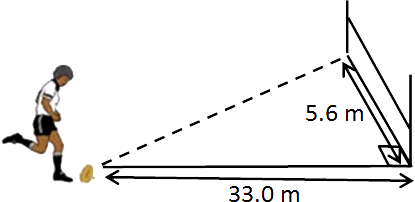
View from side
kicking-goal-diagram-1.png  
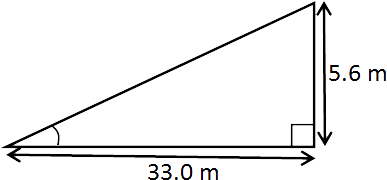
View from top
kicking-goal-diagram-2.png
[Not drawn to scale]
Tiaki is about to kick for goal.
He is kicking from the right-hand side of the goal post from a distance of 33.0 metres, as shown in the diagrams above. 
a)
The distance between the two goal posts is 5.6 metres.
Calculate how far Tiaki is from the left-hand goal post. Show all your working in the box below.
 
 

 

 

 

Tiaki is __________ metres from the left-hand goal post.
 
b)
 
Tiaki aims his kick directly at the right-hand goal post. The wind takes the ball 10° off course to the left.
i) Work out how far the ball passes to the left of the right-hand goal post. Show all your working in the box below.
 
 

 

 

 

The ball passes __________ metres from the left of the right-hand goal post.
 
 
 ii)
Does the ball pass between the goal posts?     Yes   /   No   (Circle one)

Explain your answer.
 

 
 
Task administration: 
This task can be completed with pencil and paper.
Level:
6
Curriculum info: 
Maths, Geometry and Measurement, Shape
Keywords: 
trigonometry, right angled triangles, pythagoras theorem
Description of task: 
In the context of kicking a goal at rugby, students use Pythagoras' theorem to calculate distance. Students then use trigonometry to work out if the kick passes through the posts.
Answers/responses: 

 

Y11 (09/2001)

a)

  

33.47 [Accept 33.4-33.5]

Evidence of Pythagoras' theorem z = (5.62 + 332) used, but error in calculation.

easy

very easy

b)

i)

 

 

 

 

 

 

 

 

 

 


ii)

 

Any 1 of:

  • 33tan10° = 5.82 m (also accept 5.8)
  • = tanם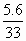 = 9.63° (also accept 9.6°)
  • sin =
    sin = 0.17 (2 d.p.)
    = 9.63°
  • cos =
    cos = 0.99 (2 d.p.)
    = 9.61°

Puts numbers into tan, sin, or cos function or uses sine rule or cosine rule but one error is made, including:

  • an error in transcribing numbers from diagram
    (or part a))
  • incorrect placement of numbers in trigonometry function or rule.

Yes, and any 1 of:

  • The angle at which the wind takes the ball off course has to be less than 9.6° to get within the goal posts.
  • The distance (5.82 m) calculated is greater than the width (5.6 m) of the goal posts.
    or
  • Accept alternative explanation if consistent with answer given in b)i).

difficult

 

 

 

 

 

 


difficult

 

 

 

difficult

NOTE: This item was trialled with students having access to Pythagoras' theorem and trigonometry ratios.