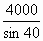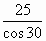Calculating lengths and heights
This task is about using trigonometry to find missing lengths.
Use trigonometry to solve the following problems.
| a) |
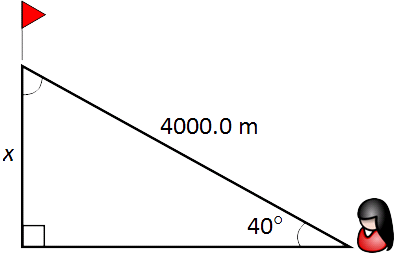
Teresa took the ski lift 4000 metres to the top of Mount Herbert, at an angle of 40º.
 [Not drawn to scale]
Calculate x, the height of Mount Herbert. Show all your working in your calculation.
x = ________ metres
|
| b) |
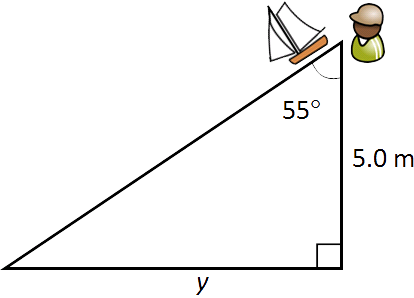
Daniel's toy boat travelled 5 metres downstream at an angle of 55° before it reached the other side of the river.
 [Not drawn to scale]
Calculate y the width of the river. Show all your working in your calculation.
y = ________ metres
|
| c) |
A penguin slid 25 metres down an iceberg at an angle of 30º until it reached the water.
 [Not drawn to scale]
Calculate z the height of the iceberg above the water. Show all your working in your calculation.
z = ________ metres
|
