Four spinners

Four spinners

Pencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Further Resources
This task is about probability.
In a game four students each have a different spinner.
Each student spins their own spinner 20 times and adds up the total of their scores.
The student with the biggest total wins.
 
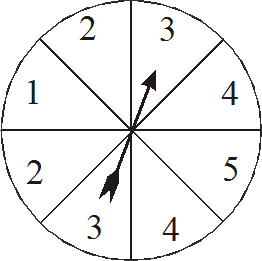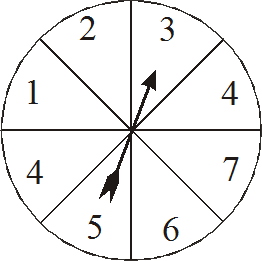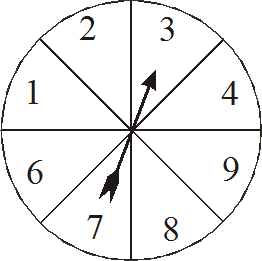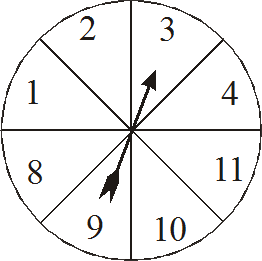vicky
wai
yvonne
zac
Vicky
 
Wai
 
Yvonne
 
Zac
 

Question

a) i) Who is most likely to win the game?

    • vicky
                    Vicky 

    • wai
                     Wai 

    • yvonne
                  Yvonne 

    • zac
                     Zac 

Question 1Change answer

ii) Explain why.

Question 1Change answer

b) Describe two different ways you could change this to make it a fair game.
1.   2.  
Task administration: 
This task can be completed with pencil and paper or online (with some automarking).
Levels:
4, 5
Curriculum info: 
Maths, Statistics, Probability
Key Competencies: 
Thinking, Using language, symbols, and texts
Keywords: 
fair games, probability, spinners
Description of task: 
Students explain who is most likely to win a game based on spinners, and how the game could be made fair.
Curriculum Links: 
Key competencies
This resource involves explaining their choice of the bias in a game of chance, and how to make the game fair, which relate to the Key Competencies: Thinking, and Using language, symbols and text.

 

For more information see http://nzcurriculum.tki.org.nz/Key-competencies
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Interpreting statistical and chance situations, sets 4-5
Interpreting statistical and chance situations, set 5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  

Y10 (08/1999)
a)
i)
 
 
 
 
 
 
 

ii)
 Zac
zac
Any 1 of:
  

•    Because the numbers on his spinner add up to the highest total.
•    The average of the numbers on his spinner is the highest.
•    Because the numbers on his spinner are the highest.

very easy
 
 
 
 
 
 
 
 
 
 
very easy
b)   Any 2 of:
  

•    By making the same pattern of numbers on each spinner.
•    By using only one spinner.
•    By everyone having a turn using each spinner.
•    By making the sum of the numbers on the spinners the same.
•    By allocating the spinners or the numbers on the spinners at random.
•    By Wai and Yvonne playing Zac and Vicky.
•    By allowing people with smaller sums on their spinners to have proportionately more spins (e.g., Vicky spins 20 times, Wai 15, Yani 12, and Zac 10).
•    By dividing Vicky's score by 3, Wai's by 4, Yvonne's by 5, and Zac's by 6.
•    Other acceptable strategies may be given.
2 correct – difficult

1 correct – very easy

Extension: The alternative strategies of making the game fair could be further explored. The last two strategies of spinning in proportion to the sum of the scores on the spinner, or dividing the score by an appropriate number are particularly interesting.