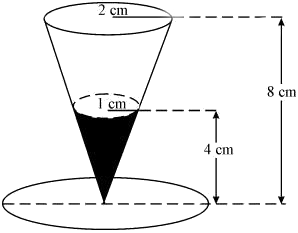
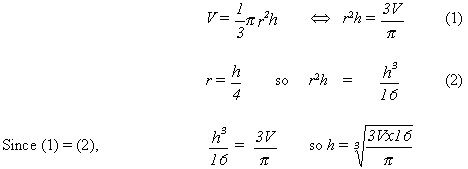Measuring cup

Measuring cup

Pencil and paperOnline interactive
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about calculating volume.
Use the information about the measuring cup to answer the questions below.

The height (h) of the cup is 8 cm.

The radius (r) of the top of the cup is 2 cm.

The volume of the cup is given by the formula:

V = 1/3πr2h (Use π = 3.14)

cone

Question 2Change answer

a)  What volume of medicine will the cup contain if it is full? cm3

Question 2Change answer

b)  What volume will be in the cup if the height of medicine is ...
     i)     4 cm? cm3 

     ii)    7 cm? cm3 

Question 2Change answer

c)  The cup had 6 cm of medicine in it.
     Monica drank some medicine, but found the cup still had 2 cm of medicine left in it.
     How much medicine did Monica drink?  cm3
Task administration: 
This task can be completed with pen and paper or online (with NO auto marking).
Level:
5
Curriculum info: 
Maths, Geometry and Measurement, Measurement
Keywords: 
volume, 3-dimensional shapes, cone
Description of task: 
Students use a diagram of, and information about a measuring cup (a cone) to calculate and answer questions about volume.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Measurement sense, sets 7-8
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 

Y10 (11/1999)

a)

 

33.49 [accept 33.45 to 33.55]

moderate

b)

i)
ii)

 4.19 [accept 4.15 to 4.25 or 0.125 × answer to a)]
22.44 [accept 22.4 to 22.5 or 0.67 × answer to a)]

moderate
very difficult

c)

 

13.61 [accept 13.55 to 13.65]

very difficult
Next steps: 

EXTENSION:

a) What depth would the medicine cup have to be to have 10 cm of medicine? (Answer: 5.35 cm)
Method of solution:
   
b) Design calibration marks for various amounts of medicine (5, 10, 15, 20, 25)
c) Graph the results of b) with depth on the y-axis and amount of medicine on the x-axis.
d) See what happens when the ratio of the height to the radius changes, i.e., the angle of the cone changes.