Hole in a prism

Hole in a prism

Pencil and paper
Overview
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about calculating volumes of composite shapes.
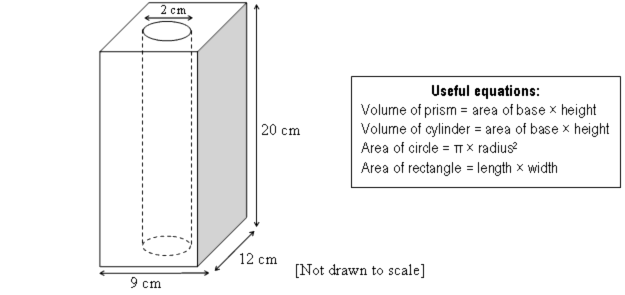
a)  Show how to work out the volume of this wooden prism before a cylindrical hole is bored through it. 
 
 
 
 
 
 
 

Volume of wood in whole prism__________ cm3

b)  Show how to work out the volume of wood remaining in the prism after a cylindrical hole has been bored through it.
 
 
 
 
 
 
 

Volume of wood left __________ cm3
Level:
5
Curriculum info: 
Maths, Geometry and Measurement, Measurement
Keywords: 
volume, cuboids, cylinders, composite shapes
Description of task: 
Students calculate volumes of composite shapes, showing their working.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Measurement sense, sets 7-8
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y10 (05/2007)
a)

Correct method for calculating the volume of a cuboid.
2160

easy
moderate
b)

Correct method for calculating the volume of a cylinder.
Correct method for calculating the volume of a composite shape
(which is 62.8 using π = 3.14).
2097.2 (using π = 3.14)
[Accept 2097-2098 as it depends on what approximation of π is used]

difficult
moderate
 
very difficult
Based on a representative sample of 155 Year 10 students. 
Diagnostic and formative information: 
  Common error Likely calculation Likely misconception
a) 41
420
288
249		 9 + 12 + 20
20 × (9 + 12)
9 × (20 + 12)
20×12 + 9		 Uses an additive or partially additive model for computing volume.
a) 108
180
240		 9 × 12
9 × 20
12 × 20		 Uses only two of the three dimensions.
b) Volume of cylinder:
251.3
40
20
80		 20 × π × 22
2 × 20
1 × 20
2 × 2 × 20		 Uses the wrong volume for the cylinder
•  Uses πr2 but with r = 2 rather than r = 1
•  Assumes area of base = 2
•  Uses half of 2 as the area of the base
•  Assumes base is a square with sides of 2cm

NOTE: Several of these misconceptions are combined, leading to a large number of different incorrect numerical responses.

Next steps: 
Using an additive or partially additive model for volume

Students need to understand that area and volume are related to multiplicative reasoning. In particular, the array model of multiplication is particularly useful.

Knowing that volume (cuboid) = width × depth × height

  • Students should firstly explore volume, starting with counting unit cubes and moving on to multiplication of the number of cuboids in each of the three directions.
    Resources Cubes and cuboids, Building buildings, How many blocks?, and Blocks in boxes help support this.
  • This should be generalised to multiplying the length of each of the three dimensions. Search for Level 4 and 5 resources with keyword: volume. Over half the resources support this model. All of these involve dimensions that are whole numbers rather than decimals or fractions.
    This extends the concept of multiplication of three numbers to obtain volume.

Knowing that volume (prism) = area of base × height 
This generalisation allows student to move away from cuboids into general rectangular prisms.

Using only two dimensions for volume
Students need to differentiate area as a square measure (i.e. multiplication of two numbers), and volume as a cubic measure (i.e. multiplication of three numbers).

Knowing the way to compute the area of a circle
Students need to know that the relationship between the radius of a circle and its area is given by πr2 - they could explore resources about area of circles.

Numeracy
For teaching the array model for multiplication which leads on to area, Book 6: Teaching multiplication and division, pp 6-7.
For teaching the array model for multiplication which leads on to volume, Book 6: Teaching multiplication and division, page 40-41.