Sides and diagonals

Sides and diagonals

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Further Resources
This task is about looking at patterns in polygons and writing rules to describe them.

In any polygon the number of diagonals coming from one corner can be worked out by subtracting three from the number of sides.

  
 

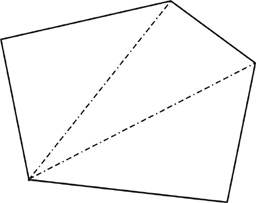
So this polygon, with five sides, has two diagonals from any one corner.
 

a) i)
How many diagonals from one corner would a shape with 57 sides have? __________
 
  ii)
How many diagonals from one corner would a shape with k sides have? __________
 
  iii)
If a shape had 100 diagonals from each corner, how many sides would it have?
 
__________
 
b) i)
How many triangles are formed altogether by the two diagonals in the figure above?
 
__________
 
 
ii) 
 
 How many triangles would a shape with 49 sides have? __________
 
 
iii)
 
 How many triangles would a shape with q sides have? __________
 
c)
Find a rule connecting the number of diagonals with the number of triangles formed.
 
 

 

Task administration: 
This task is completed with pencil and paper only.
Level:
5
Curriculum info: 
Maths, Number and Algebra, Patterns and relationships
Key Competencies: 
Thinking
Keywords: 
spatial patterns, functional rules, linear equations, problem solving
Description of task: 
Students respond to questions about the relationship between diagonals, triangles and polygons; then write a rule to describe the pattern.
Curriculum Links: 

Key competencies

This resource involves identifying and implementing strategies to a solve multistep problem. This relates to the Key Competency:Thinking.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Patterns and relationships, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y10 (09/1998)
a) i)
ii)
iii)		 54
k – 3
103		 easy
moderate
moderate
b) i)
ii)
iii)		 3
47
q – 2 [or the equivalent, i.e., (q – 3) + 1]		 very easy
moderate
difficult
c)   Any 1 of:

•   The number of triangles is one more than
     the number of diagonals.
•   T = 1 + D or D = T – 1
•   The number of diagonals is one less than
     the number of triangles.
•   There is one fewer line than the
     number of triangles.
•   Other correct statements.

 difficult