Alien shape patterns

Alien shape patterns

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about finding a rule for a growing pattern.
Gerry is using matchsticks to make "alien" shapes.  He has made three so far.
 
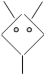Alien pattern 1
Alien pattern 2
Alien pattern 3
Alien 1 Alien 2 Alien 3
 
a)
Draw Alien 4 in the space below.
 
 
 
 
 
 
 
 
 
b)
Complete the following table.
 
Alien number 1 2 3 4 5 7 9
Number of matches used 7            
c)
Describe, in words, the rule which links the Alien number to the number of matches used.
 
 
 
 
 
d)
Using x for the Alien number and y for the number of matches, write your rule as a formula.
 
y =__________________________________
 
e)
Show how to use your formula to work out the number of matchsticks needed for Alien 21.
 
 
 
 
 
Number of matchsticks used: ________
Task administration: 
This task is completed with pencil and paper only.
Level:
5
Curriculum info: 
Maths, Number and Algebra, Patterns and relationships
Keywords: 
spatial patterns, functional rules, rules, linear equations
Description of task: 
Students complete a table then describe and write a rule to work out the number of matchsticks needed to make alien shape patterns.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Patterns and relationships, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y10 (09/2008)
a) Correct drawing very easy
b)
Alien Number 1 2 3 4 5 7 9
Number of matches used 7 11 15 19 23 31 39

All numbers correct
or
1-2 errors
 
 
 
 
difficult *1

very easy
c) Multiply the alien number by four and add three
or
Any other rule that correctly relates the Alien number with the Number of matches.		 moderate *2
d) y = 4x + 3 or
y = 4(x – 1) + 7 or
any equivalent functional rule.
Accept a rule that is the inverse of this, e.g., x = (y – 3) ÷ 4		 moderate
e) 87 matchsticks
Working that shows any 1 of:
Using the formula from part d) (functional approach);
Successive addition of 4 for each new alien number (recursive approach); or
Other correct strategies.		 moderate
easy

Based on a representative sample of 161 students

NOTE:

  1. Students did not look carefully at the Alien number in the last 2 columns. 
  2. In parts c) and d) only functional approaches are acceptable as this is what the wording of the question specifies. This makes them harder than the working in part e) which allows the recursive approach (i.e., successively adding on 4).
Diagnostic and formative information: 
  Common error Likely misconception
b) 11, 15, 19, 23, 27, 31 Incorrect reading of the table
Ignoring the Alien numbers given in the table (7 & 9) and using 6 & 7 instead.
c)
d)		 Descriptions or rules that are based on successive addition of 4. Recursive approach
The students use successive addition (recursion) rather than giving a functional relationship (i.e., relating the alien number to the number of matches used). See Strategies box.
e) 79 Combination of the above two errors.
e) 84 Ignores the intercept
Ignores the three matches that are present irrespective of the Alien Number.

 

Next steps: 
Incorrect reading of the table
Encourage students to read the information in tables (and graphs) very carefully. This is a common cause of misinterpreting graphs and tables as well as a common way of designing graphs and tables that are misleading.

Recursive approach
Students at this stage need to move beyond just a description of the number of extra matches needed. This relationship works horizontally across the table, and is referred to as the recursive approach.

Encourage students to use the functional approach, which asks for the students to describe the relationships vertically. Functional relationships in patterns can be explored by students exploring the relationship between the cardinal position of a pattern and the value for that position.
For example using spatial patterns and the number of ice block sticks make up the nth shape. 
Explore some resources that explore the relationship between spatial patterns, number patterns and functional rules.

Functional relationships can also be explored by looking at "computing machines" where numbers are inputted and then outputted, e.g., Number machines or Number machines II.

For further information and resources about functional thinking with regard to patterns click on the link Algebraic patterns concept map: Functional thinking.

Ignores the intercept
Students need to recognise that there are three matches which are present regardless of the Alien number. This could be recorded as an extra column at the left-hand end of the table with an Alien number of 0. Plotting all the points in the table and joining the points will show that the line cuts the y-axis at the point where y (number of matches) equals 3. This point is referred to as the intercept of a straight line.

Click on this link  for resources which test students' understanding of the concept of intercept.


Strategies
Continuing patterns of this type can be expressed in two different ways:

Functionally.
This relates the number of matches to the alien number. This is equivalent to working vertically in the table, relating one number to the number immediately above it. This can be expressed in words or symbolically.

Example
"The number of matches is the alien number times four and then add three." or 4x + 3

Recursively
This relates the number of matches in a shape to the number of matches in the previous shape. This is equivalent to working horizontally in the table, relating a number to the number immediately to its left. This can be expressed in words or symbolically.

Example "The number of matches is the number of matches in the previous shape plus four."

No students i nthe trial expressed this relationship symbolically.

The recursive approach is still a valid one, and becomes very useful in more advanced mathematics. More able students will be able to cope with algebraic representations of recursive relationships, such as adding on 4 to get the next term. The alien example can be formally described recursively as:
     x0 = 3
     x1 = x0 + 4;    x2 = x1 + 4;    x3 =  x2 + 4;   x4 = x3 + 4;  or more generally xn+1 = xn + 4.

 

Success rates
Part e)
There were three different correct strategies that trial students used in part e). They were as follows:

  1. Direct substitution into the equation (functional)        4x + 3 = 4 × 21 + 3 = 87           
  2. Evaluation of sub-steps of the equation (functional)  4 × 21 = 84;     84 + 3 = 87. 
  3. Successive addition of 4 (recursive)

The more mathematically able students tended to use direct substitution into the equation (Method 1 above). They had a success rate of 96% for obtaining the correct answer of 87 matches for part e).

More average ability students tended to use sub-steps (Method 2). They had a success rate of 83%.

Students who used successive addition (Method 3) tended to be mathematically less able than those using the other strategies. Their success rate was only 20%.

Click on the link for further information about patterns in the Algebraic patterns concept map.