Walking to school
Justin was late to school. Your teacher will read out Justin's reasons for being late to school and where they happened.
- Cut out the boxes below
- Place the boxes on the line as your teacher reads out what happened to Justin.
- Check to see the boxes are in the right order.
- Glue the boxes on.
- This resource looks at developing understanding of ordering basic fractions.
- Students could be asked to explain how they know that one fraction is larger/smaller than another when they are placing them.
- Some students may be able to identify the order of the fractions without cutting out and comparing the fractions before ordering.
- Encourage students to check the order before gluing the fraction down.
- Select appropriate pace and repeat if necessary – this context is intended to scaffold students to putting fractions on a number line and the delivery and pace should also support them.
Read the following text:
Justin is walking from his home to school. When he got to school he was late. He told his teacher things that had happened on the way to school, but not in the order they had happened. Listen carefully as I read out Justin's reasons and where they happened.
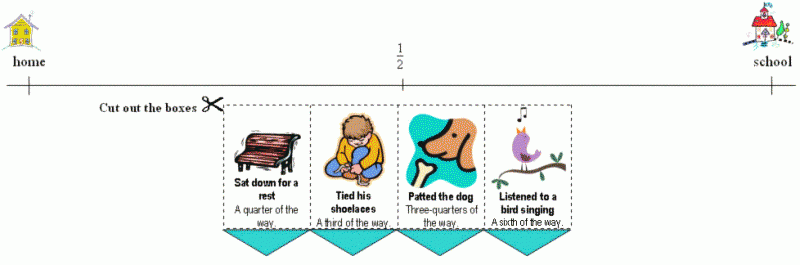
- One-quarter (1/4) of the way to school he sat on a park bench for a rest.
- One-third (1/3) of the way to school he stopped to tie his shoelaces.
- Three-quarters (3/4) of the way to school he stopped to pat Max the dog.
- One-sixth (1/6) of the way to school he stopped to listen to a bird singing.
- Bird 1/6 (4cm from home);
- Rest 1/4 (6cm from home);
- Shoelace 1/3 (8cm from home);
- Dog 3/4 (18cm from home).
NOTE: Accept accuracy of plus or minus 0.5cm or ask students to explain how they knew where to put the mark.
| Common error | Likely misconception |
| 1/3 , 1/4 , 1/6 , 3/4 |
Whole number (larger numbers) Ordering fractions by the larger the numbers the larger the fraction. |
Based on a trial set of 22 Y5 students.
NOTE: Students should be able to order all 4 fractions to indicate understanding of ordering simple unit fractions.
After cutting out and placing the fractions, students could be asked to mark down which fractions they started with to work out the order, i.e., did they start with 1/2 and then halve to get 1/4 , or did they start with 1/2 then 1/3 , 1/4 , 1/6 . By sharing their strategies for ordering the strategies can be critiqued to find the easiest or most efficient.
Understanding partitioning and the part-whole relationship
Students who have a whole number misconception about ordering fractions need to understand that a fraction describes the relationship between the part and a whole before trying to devise a system to compare or order fractions. If required, students could go back to partitioning and explore constructing the parts (unit fractions), combining these parts to make non-unit fractions that are between 0 and 1 (called proper fractions), and naming these new fractions (part-whole fractions). Encourage students to explore a range of many new fractions such as 3/7 , 5/8 , etc, or even include some top heavy (or improper) fractions and discuss how large these fractions are.
Using diagrams to compare
After this, encourage students to compare just two fractions (including non-unit fractions) before trying to order a number of unit and non-unit fractions. For example, students could explain (using materials, diagrams or reasoning) how they know the larger of 1/2 and 1/6 , and then the larger of 2/3 and 1/5 . Appropriate drawing of fractions can promote understanding and help with comparing the size of fractions. For a resource comparing fractions see NM0137: Larger fractions (level 2).
Simple fractions correctly placed
For students who correctly placed all simple fractions, it is important to ensure that they do not develop the misconception that fractions are always between 0 and 1. Ask students if someone jumped where a fraction such as 5/4 would be. Students could draw this on another number line and start to look at where other fractions such as 1/4 , 3/4 , 5/4 ; or 1/2 , 2/2 , 3/2 might go. Scaffold the students to construct these top heavy fractions by starting with the unit fraction of each and asking for non unit fractions with the same denominator. Try different fractions, 1/5 , 3/5 , 6/5 and even strange fractions such as 7/11 .

Other resources
- For similar ARB resources click on the link use the keywords, fractions AND number lines.
- For ARB resources about comparing fractions click on the link or use the keywords fractions AND ordering numbers.
- Click on the link for further information about Fractions and number lines (Fractional thinking: conceptual map).
Numeracy resources
Book 7: Teaching Fractions, Decimals and Percentages, 2006:
- Fraction circles, (p.9), Advanced counting/early additive part-whole
- Trains (p.19) Early additive/Advanced additive/Early multiplicative.

