Ziggurat formula

Ziggurat formula

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about using equations to work out attributes of a ziggurat shape.


 

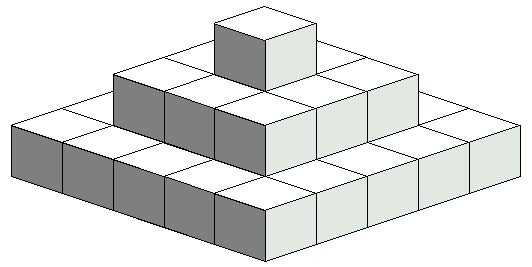
This shape is called a ziggurat and is three blocks high (n = 3). Each block is 1 metre high.
 
Here is a rule for the number of blocks in a ziggurat that is n blocks high:
 
bn =  n is the height of the ziggurat.
bn is the number of blocks in a ziggurat that is n blocks high.
 
a) How many blocks are there in a ziggurat that is
 
 
i)
 
ii)
3 blocks high? __________
 
12 blocks high? __________
 
Each face on a block in the ziggurat has an area of 1 m2. This formula gives the total surface area for ziggurats of different heights:
 
an = 8n2 - 4n + 1

n is the height of the ziggurat.
an is the total surface area (in m2) of a ziggurat that is n blocks high.
 
b) What is the total surface area of a ziggurat that is
 
 
i)
 
ii)
3 metres high? __________ m2
 
10 metres high? __________ m2
Task administration: 
This task is completed with pencil and paper only.
Level:
5
Curriculum info: 
Maths, Number and Algebra, Equations and expressions
Keywords: 
substitution, equations, spatial patterns
Description of task: 
Students use substitution into equations to evaluate the number of blocks and total surface areas in shapes of different heights. The stimulus can be used as a challenging task to try and derive the rules from the spatial pattern. This is classified as Patterns and Relationships.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Patterns and relationships, sets 6-7
Using symbols and expressions to think mathematically, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 

Y10 (10/2000)

a)

i)
ii)

35
2300

moderate
difficult

b)

i)
ii)

61
761

difficult
difficult
 
NOTE: In b) the surface area excludes the base. Including the base, the surface area is 12n2 - 8n + 2
 
Extension:
Diagnostic and formative information: 
  

Common error

Likely calculation

Likely reason

a)i) 
   ii) 

575 
36 860 

(123 - 3) ¸ 3
(483 - 12) ¸ 3

Treats 4n3 as (4n)3.

a)i) 
   ii) 

565 
6361 

242 - 12 + 1
802 - 40 + 1

Treats 8n2 as (8n)2.

 

Next steps: 
Extension

a) i)
ii)		 What is the height of the tallest ziggurat that can be built with 1500 blocks? (Ans = 10)
How high is a ziggurat that has a surface area of 481 m 2? (Ans = 8)
 
b) For each of the 8 surface areas below, find out how high the ziggurat is by using factorisation rather than trial and error. Look for the patterns in the factorised equations.
Surface area = 5, 25, 61, 113, 181, 265, 365, 481
 

 

 Answers      
 

Surface area 

 Factorised  Equation  Positive solution
  5 
25 
61 
113 
181 
265 
365 
481 		 8n2 - 4n - 4 = 0
8n2 - 4n - 24 = 0
8n2 - 4n - 60 = 0
8n2 - 4n - 112 = 0
8n2 - 4n - 180 = 0
8n2 - 4n - 264 = 0
8n2 - 4n - 364 = 0
8n2 - 4n - 480 = 0		 (8n + 4)(n - 1) 
(8n + 12)(n - 2) 
(8n + 20)(n - 3) 
(8n + 28)(n - 4) 
(8n + 36)(n - 5) 
(8n + 44)(n - 6) 
(8n + 52)(n - 7) 
(8n + 60)(n - 8) 		 n = 1 
n = 2 
n = 3 
n = 4 
n = 5 
n = 6 
n = 7 
n = 8 
 
c) 		  
Give the ziggurat problem and let the students find the equations for the number of blocks or the surface area as a function of the height (n).