Spin a surprise

Spin a surprise

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about how likely things are to happen.
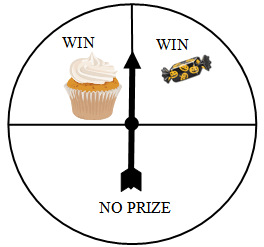
Sharni spins the arrow to see if she wins a prize at her school gala.
 
a) i)
Which of these is true? (circle one)
 
    (A) 
Sharni is more likely to win a sweet than a muffin.
    (B)
Sharni is more likely to win a muffin than a sweet.
   
(C)
 
Sharni is just as likely to win a muffin as a sweet.
 
  ii)
Explain your answer.
 
 
 
 
 
 
 
b) i)
Tana has a spin. Which of these is most likely? (circle one)
 
    (A)  Tana wins a prize.
    (B) Tana does not win a prize.
   
(C)
Tana is just as likely to win a prize as he is to not win one.
 
  ii)
Explain your answer.
 
 
 
 
 
 
Task administration: 
This task is completed with pencil and paper only.
Levels:
2, 3
Curriculum info: 
Maths, Statistics, Probability
Keywords: 
probability, independence, work samples
Description of task: 
Students recognise equal and different likelihoods when playing a game of chance.
Curriculum Links: 
This resource can be used to provide one source of evidence to suggest students' understanding of comparing and explaining likelihoods of outcomes for simple situations involving chance.​
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Interpreting statistical and chance situations, set 3
Interpreting statistical and chance situations, sets 3-4
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
      Y5 (05/2010)
a) i)
ii)

 

 D
Any 1 of:

  • Statements giving the equal chances (both 1/4 ; 50:50 etc.); e.g., because they're both 25 25 chance (i.e., both have 25% chance).
  • Statements about the fraction that each segment takes up; e.g., they both have a quarter of the circle.
  • Statements that the areas are equal, e.g.,
    The space is equal in the sweet and muffin.
    Both prizes are the same size.
    The muffin and the sweet are the same amount [of area].
 moderate
difficult

 
b) i)
ii)

 

 D
Any 1 of:

  • Statements giving the equal chances (both 1/2 ; 50:50 etc.); because they're both 50 50 chance (i.e., both have 50% chance)
  • Statements about the fraction that each segment takes up; e.g.,
    They both have a quarter of the circle.
    Half of it you will get a prize and the other half not. So it's equal.
    Half of the wheel has prizes and the other half doesn't.
  • Statements that the areas are equal.
 moderate
very difficult

 
Based on a representative sample of 153 students.
 
NOTE: If the student make statements about the position of the spinner, check that they understand that this is the beginning position before the arrow is spun. They may then wish to amend their answers. This resource looks at uncovering students' conceptions and misconceptions in probability reasoning. The explanation is more revealing of students' thinking than the multiple choice response.
Diagnostic and formative information: 

There are many well known misconceptions about probability. Examples of these follow.

For more information click on the link Probability concept map: Common misconceptions.

The letters [A], [B] or [C] in each example below is the response the student chose in the multiple choice part of that question.

  Likely misconception
a) - b) Outcome misconception
Some students may respond to situations involving chance by stating that you just can't tell anything when it comes to probability.

  • You don't know what is going to happen really [C].
  • Because you never know if you are going to win a prize or not [C].
  • Because you're not completely sure if you win or not [C].
  • On spin the bottle you never know what you are going to get [C].

a) - b)

 

 Influence misconception
Students believe that previous events can be influenced by a range of factors. For example, the outcome of a coin toss may depend on what the previous toss was.

The way the spinner is spun

  • Because it is more likely to move to the right than to the left [A].
  • Because he might have a stronger arm [A].
  • If you did it cafly (carefully) to win a prize [A].
  • Because what if the arrow goes slowly [clockwise] and lands on the sweet [A].
  • Because if she spins it more to the left she is more likely to win a muffin [B].
  • Because its anlikely to turn right around [B].
  • Well most ley you spin it right so it will stop on the left [B].
  • Because he will be strong so it will be more likely that he won't win a prize[B].
  • Its mire likely to turn a quarter the way around [B].

What the person wants (or needs) to happen

  • Because she probely wouldn't want the chocolate [A].
  • If Sharni wanted a muffin and she trys to win she will not get it. She will get the sweetie [A].
  • Because everyone likes prizes [A].
  • Because he doesn't need a prize [C].
  • She thinks she will win but she sound neves [nervous] [C].
  • Win a prize so he could make his friend Jelious [A].

The original position of the spinner has an influence

  • Because the arrow starts in the middle so it is more likely to land in the middle [C].
a) 
Lack of independence /  Negative regency misconception (previous outcomes have an influence) 
  • People often think that if an event has not happened for a while then it is more likely to occur at the next trial.
  • Because he has not win a prize [A].
  • Because it has already landed on no prize [A].
a) - b)

 
Assumes spinner finishes where it started (see NOTE under the scoring guide)
  • She should get a muffin and a sweet because she landed in the middle of them [C].
  • Its kinda in the middle, but its sorta more on the muffin [C].
  • I't between win, win so she wins both [C].
  • The arrow was egzukuly in the mitul [C].
  • Because its between the muffin and sweet [A].
  • Because it is not on no prize [A].
b) Equiprobability misconception
The student sees events as equally likely even when they have different probabilities.

  • Because instead of one thin[g] there are 2 prizes to win and one [that doesn't win] [A].
a) - b)
 
 
 
 
 
 
 
 
Availability misconception
Features of the prize: It is bigger, nicer, worth more etc.,
  • Because the sweet looks bigger [than it should relative to the muffin] [B].
  • Because a sweet is much nicer than a muffin [A].
  • I chose it because a muffin is more worth it for a little sweet [B].
  • I pick muffin because it has cream in it [B].
  • Because prizes is yum to eat and it sondles yemy [yummy] [A].
a)

 

 States what the prize will be (with no justification)

  • The arrow is going to land on the muffin [B].
  • Compares "No prize" with only one of the two prizes
  • Not winning a prize is bigger [B].
  • Because the space for no prize is huge [B].
Next steps: 

Each of these probability misconceptions above is common, even with adults.

There are three main ways we suggest can help students overcome their incorrect ideas. 

  1. Have discussions between students. Get them to justify their own explanations and to critique the explanations of others. Click on the link Mathematical classroom discourse for more ideas on how to do this. 
  2. Have plenty of practical experiences of probability, and record the results of this. Increasing exposure to and experience of probability builds up an intuitive feel for chance. 
  3. Find ways to quantify probability. This should be with simple counts for fixed sample sizes at these year levels.
For more information about probability, go to the ARB Probability concept map.