Matchstick patterns III

Matchstick patterns III

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Further Resources
This task is about continuing a pattern and describing a rule.

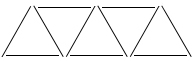
Shape A           Shape B                   Shape C       

a) Use your matchsticks to make the next two shapes in this pattern. When you have made the shapes either show them to your teacher or draw them in the boxes below.
 


Shape D                                        Shape E
 
b)
Write the rule that explains how many extra matchsticks you need for each new shape in the pattern.
 
 
 
c) Fill in the table below to show how many triangles there are in each shape and how many matchsticks have been used. The answers for Shape A have been written in for you.
 

i) Shape A makes triangle out of  matchsticks.
ii) Shape B makes triangles out of matchsticks.
iii) Shape C makes triangles out of matchsticks.
iv) Shape D makes triangles out of matchsticks.
v) Shape E makes triangles out of matchsticks.
 
d)
 
 
Describe the rule that explains the relationship between the number of triangles and the number of matches needed.
 
 
Task administration: 
This task is completed with pencil and paper, and other equipment.
 
Equipment:
25 matchsticks (or equivalent, e.g., ice block sticks) per student.
 
Students may complete part d) by verbally explaining their rule rather than writing it down.
Level:
4
Curriculum info: 
Maths, Number and Algebra, Patterns and relationships
Keywords: 
spatial patterns, number patterns, functional rules
Description of task: 
Students use matchsticks to continue a triangular spatial pattern and write a rule to describe the number needed for each pattern. They then complete a table and a rule to show the relationship between the number of triangles and the number of matchsticks.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Patterns and relationships, sets 5-6
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 

 

a)

  
Shape D
 
Shape E

b)

  

Accept any explanation that includes the idea of "adding on 2" each time.

c)

ii)
iii)
iv)
v)

2,5
3,7
4,9
5,11

d)

   For any 1 of:

  • Multiply the number of triangles by 2 then add 1 (2n + 1).
  • Multiply the number of triangles by 3 then take off 1 less than the number of triangles (3n - (n - 1)).
  • Multiply one less than the number of triangles by 2 and add this to 3 (3 + 2 (n - 1)).
  • Other equivalent rules.