Painting a water tank

Painting a water tank

Pencil and paper
Overview
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about calculating the surface area of the sides and top of a cylinder.

Area of circle = πr2
Circumference of circle = 2πr
Volume of cylinder = area of base × height
 Area of rectangle = height × length

 

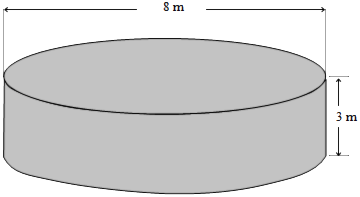
Jordan painted this water tank with one coat of paint.

  • First he painted the top.
  • Then he painted the sides.

Show how to work out the area he painted (show all of your working, including any diagrams).

 

 

 

 

 

 

 

 

The area Jordan painted was __________ m2  
Level:
5
Curriculum info: 
Maths, Geometry and Measurement, Measurement
Keywords: 
area, surface area, cylinders, circumference, work samples
Description of task: 
Students calculate the surface area of the sides and top of a cylinder, showing their working.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Measurement sense, sets 7-8
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y10 (11/2009)

Working
Students need to perform three different steps to answer this question.

  • Shows how to compute area of the top using πr 2, (with r = 4).
  • Shows how to compute the area of the side by:
    a) Showing how to obtain the circumference of the top of the tank using length = 2πr or πd (with r =4, or d=8), and
    b) Multiplying circumference by height to get the area of the side.
  • Adds the two areas together [accept even if the areas have been worked out incorrectly].

Annotation of working 
This is when the student writes what their working stands for, for example "Area of the top", etc. Annotation was not asked for, but correlates with getting a correct answer. Good annotation allows the working to be more easily followed by others. See Examples of student working at the end of this resource.

  • Gives full annotation of working.
  • Gives a reasonable amount of annotation.
  • Any annotation.


Answer

  • 125.663 or 40π
    [Accept answers from 125 to 126 to take account of different values of π, and of rounding to the nearest whole number].
    Almost all students who got all their working correct got a correct answer.

 

easy
moderate

moderate

very difficult
difficult
moderate

difficult
Based on a representative sample of 136 Y10 students.

NOTE: Accept each stage of the working if the method used for it is correct (e.g., πr 2) even if some numerical calculation errors are made
Diagnostic and formative information: 
Common response Likely misconception

Area of top =πd =25.1 [This leads to answers close to 75.4]
Circumference =  πr 2 =50.27

 Confuses the area of a circle and the circumference of circle

Area of top =πd 2 (201.1)
Circumference = πr, 2πd

 Confuses radius and diameter

Area of top = (πr)2, (πd)2, πd.2, πr.2

Misapplies formulae (including either of above misconceptions)
Students do not know the convention for squaring numbers, or of the order of operations.

Area of side = area of top × 3
[including answers close to 150.8]
or
Area of side = 8×3 = 24
or
Total area = 8×3 = 24
or
Adds areas and volumes to get the total area.

Confuses area and volume or cannot visualise the 3-D shape
These students do not recognise the area of the side involves the circumference × height.
This is often done in conjunction with the above error, but some students who calculate the area of the top correctly make this error.
Area of top = 8

Cannot visualise the 3-D shape
Students use the given diameter as if it was the area of the top.

Area of top + Area of side + Area of bottom
or
Other addition of areas

Adds incorrect components to obtain the surface area - cannot visualise the 3-D shape
The first of these indicates that the student sees the bottom of the tank being painted.
Other area calculations may indicate a lack of 3-D visualisation.

Student strategies

Students who used full or partial annotation of their working were more successful at getting all or nearly all of the stages of the problem correct. Fifty percent of those who gave full annotation had all component correct, as did nearly fifty percent with a reasonable amount of annotation. Only about twenty five of percent those with little or no annotation got all components of the problem correct. See Examples of student working for exemplars of student work.
Next steps: 
Misapplies formulae
Students who misapply formulae need to know:

  1. the meaning of "squared", so r2 = r × r (and it is not r × 2); and
  2. the BEDMAS rule for order of operations. This means that the r should be squared before multiplying by π. For resources on this use the keyword or click on the link; order of operations.

Confuses the area of a circle and the circumference of circle
Students need to be clear that:

  1. circumference is a measure of length, which means that it should be measures in metres (m). Only one length measure (diameter or 2 × radius) should be used in its calculation; and
  2. area is a square measure such as square metres (m2). It should therefore include multiplying two lengths together. Students may know that a rectangle has an area = width × height, each of which is measured in metres, so the result is measured in square metres (m2). This is the effect of the r2, because r is measured in metres.

Students could explore circumferences (click on the keyword or use the link; circumference); or
Explore area of circles (click on the keyword or use the link; circles AND area).

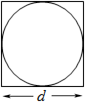
Confuses radius and diameter
This is a basic geometric knowledge issue. One easy way to see that πd 2 is incorrect is to draw a square around the circle. The area of the square is d 2 so the circle must be less than this, i.e. πr 2.

Confuses area and volume
Students need to be clear that:

  1. area is a square measure such as square metres (m2). It should therefore include multiplying two lengths together.
  2. volume is a cubic measure such as cubic metres (m3). It should therefore include multiplying three lengths together.

Cannot visualise the 3-D shape

  1. Students need to be able to visualise that the side of the tank is in fact a long, thin rectangle. It has a length equal to the distance around the circle (the circumference), and a height of 3 metres
  2. Students could make a 3-D model by cutting out a circle of diameter 8 cm (radius 4 cm and use a compass). They could then cut out a long rectangle that is 3cm wide, and wrap this around the outside of the circle. This leads to the equation circumference × 3 for the area of the strip.

Examples of student working
The following show successful or nearly successful strategies for solving the problem with the working displayed. They show different levels of annotation of what each of the formulae represent (e.g. "side of tank", "length around the top of the tank" etc.). Some employ the use of diagrams as well. The most effective diagrams had the relevant dimension displayed on them.


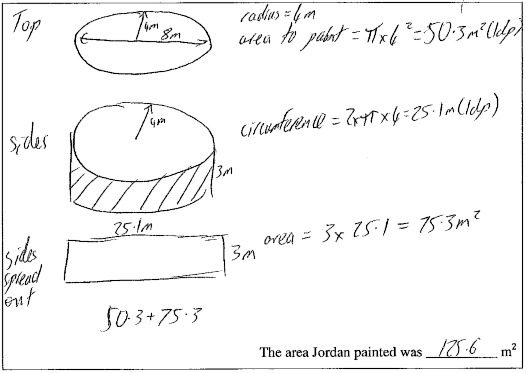
High level of annotation including the use of 2-D and 3-D diagrams with relevant dimensions displayed.

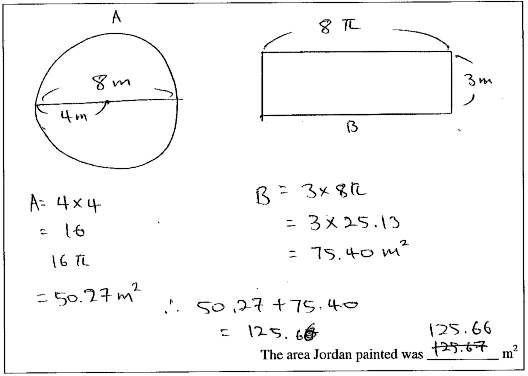
Low level of annotation but good use of 2-D diagrams with relevant dimensions displayed.

High level of annotation including the use of 2-D diagrams without the relevant dimensions displayed.

High level of annotation including the use of 2-D diagrams without the relevant dimensions displayed. Sophisticated use of π.

Low level of annotation. Includes an error in the calculation of the side length. Full credit for working was given, but the student got no credit for their answer.

Clearly shows calculations used and a correct answer, but with no annotation.