Repeating bead patterns II
| Y6 (11/2010) | ||
|
a) i) ii) |
14 7 |
moderate easy |
| b) | 4 | easy |
| c) | 12 | easy |
| d) |
 |
easy |
| e) |
An explanation involving any 1 of:
|
moderate |
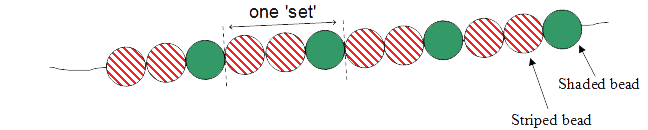
This resource is about identifying the underlying rule for repeating patterns and using this to calculate the number of striped or shaded beads for any given number of sets – or the number of striped beads in a pattern given the number of shaded beads (or vice versa). Being able to work these out is an indication of the beginning of functional thinking or developing a generalised algebraic rule. This involves being able to derive a functional or direct rule for a pattern (e.g., how many striped and shaded beads do I need for 20 sets?). Students who talk about adding two each time are describing a sequential (or recursive) rule.
| Common response | Likely misconception | |
|
a) i) ii) |
8 and 4 |
Counting the beads on the diagram Students have not worked out the number of beads for 7 sets, they have worked out (or counted) the number of each bead in the diagram at the top of the resource. A quarter of students made this error |
|
a) i) & ii) |
56 and 28 |
Using the diagram as a set rather than the set indicated. Students have assumed that the diagram of 12 beads represents one set of beads rather than the illustrated 'set' of three beads. |
|
b) & c) b) & |
16 3 8 |
Applying incorrect rule – did not use the correct ratio of shaded to striped beads Reversed the rule and multiplied the striped by 2 instead of the shaded. Reversed the rule: divided the shaded by 2 instead of the striped. Students indicated that the same numbers of striped and shaded beads were needed, rather than two striped beads for every one shaded bead. This is likely to be similar to the above misconception |
| d) |
 |
Using an incorrect sequential relationship to complete the table Students write the numbers of beads needed, but ignore the set numbers already in the table, and increments the rows sequentially. |
| e) |
e.g., The striped beads are double the shaded beads and the shaded beads are half the striped beads |
Incomplete/insufficient explanation In their explanations students do not identify how to work out both the striped and shaded beads from the set or gave a sequential rule (add two every time) which cannot be used for larger numbers of sets such as 150 sets. |
Counting the beads on the diagram
Students who counted the beads in the diagram and gave this as their answer may have:
- a misunderstanding about the question (reading error) or
- do not know how to work with repeating patterns.
For a possible reading error ask the students what they were finding out. This should reveal that they did not read that Maraea was looking at 7 sets and a set was identified as three of the beads (two striped and one shaded). It may also reveal that they did not pick up on the idea of repeating sets to make repeating patterns.
For not knowing how to work with repeated patterns students may need to explore and construct simple repeating patterns [Repeating patterns] and describe how they work (rules for construction) before trying to look at the relationships between the variables (striped or shaded) and the numbers of sets (which moves into functional type relations). Students could look at some basic repeating patterns in the resource, Necklace patterns.
Using the diagram as a set rather than the set indicated.
Students who used the whole diagram as the 'set' are likely to have made a reading error. A number of these could then correctly calculate the number of striped and shaded beads (7 × 8 and 7 × 4, respectively). This may relate to students not knowing that a repeating pattern is a construct of a repeated unit (or set). Ask these students to explain what a set might be in the repeating pattern and refer them to the diagram if necessary. If this is not sufficient they could explore by making up a repeating pattern and indicating how the unit of repetition (set) works.
Applying incorrect rule – did not use the correct ratio of shaded to striped beads
These students did not correctly apply the rule of relationship between the number of sets and the striped and shaded beads. They could be asked to use their rule to check the numbers of striped and shaded beads with different numbers of sets. This kind of exploration could be supported by the resource, Necklace patterns.
Using an incorrect sequential relationship to complete the table
These students assumed that the sequence of sets in the table continued 1, 2, 3, 4, 5, 6, etc and used a sequential strategy to solve for those numbers. This error could be a reading error and it is likely that students will only need to be directed to check the number of sein the table to correct their own work. The purpose of this resource is to encourage students to think about the patterns in terms of how many striped/shaded beads there are for each set, rather than 'sequentially'. Numbers like 10 and 40 support this.
Incomplete/insufficient explanation of how to work out the number of striped or shaded beads from the number of sets
Encourage the student to identify what is happening from one shape to the next to develop a sequential idea of how the pattern grows. The resource, Continue the patterns looks at developing repeating patterns and explaining the rules at Level 3. Students could share their rules for the patterns in small groups and check that each others' rules work for all members of the pattern. Once students can identify the sequential rule they could look at developing a functional rule (see Description of a sequential rule below).
Description/explanation of a sequential rule or counting in 2s or 1s
For students who described a sequential rule, ask them how they might find a rule that would work for any given number, e.g., How many sticks for shape 100? Trying to use the sequential rule is unwieldy and the need for a functional rule can become evident. Additionally, as students apply their sequential rule they may see the connection between the number they are adding on to the previous shape and the coefficient of n (shape number) of the functional rule. Explanation does not refer to the number of sets and both striped and shaded beads
Students who did not refer to both variables (striped and shaded) may simply need to be asked about the other variable. As the number of shaded beads matched the number of sets, they may have felt it was self explanatory. They could be asked to describe the pattern for a different repeating pattern.
Providing a sufficient explanation – Peer assessment
Many of the students gave explanations that were just sufficient, but did not fully describe or explain how they worked it out. These students could share their explanation (or explanations from this resource) in a group to identify details and clarify ideas that are needed in their explanations. Students could develop criteria for an explanation and do some peer assessments. They could also have a "sufficient" explanation modelled and made explicit to them. The criteria might include the following ideas written in students' own words:
- specific details;
- appropriate use of or reference to examples;
- justification;
- clarity to another reader.
Click on the link to the English resource Writing an explanation for further information or ideas about supporting self-assessment.

