|
|
Recursive (sequential) strategies |
|
|
|
Explicit (functional) strategies |
|
Introduction |
Algebraic Patterns |
|
|
|
|
|
|
|
Repeating patterns |
|
Functional relationships |
|
|
|
|
Using repeating patterns to think functionally |
|
The study of patterns is a key part of algebraic thinking. It is important that students are able to recognise and analyse patterns and make generalisations about them.
Patterns can be created from shapes, sounds, colours or numbers. Patterns can be visual or spatial. They can be repeating (A B B A B B A B B A...) or they can be sequential (1, 4, 7, 10, 13...). Students can continue a given pattern, find the missing element or elements in a pattern, or make up their own pattern. Patterns can also be analysed and general rules created to describe the patterns. Work with number patterns helps develop facility, flexibility and familiarity with numbers as well as building understanding of general number properties.1 Work with patterns also allows students to develop logical reasoning skills, make conjectures, and test their ideas about them.2
Pattern exploration leads logically to the development of rules to describe the pattern and strategies to work out subsequent members of a given pattern.
1 Stacey, K. and M. Macgregor (1997). Building Foundations for Algebra. Mathematics Teaching in the Middle School 2(4): 252-260
2 Ibid, Meeks Roebuck, K. I. (2005). Coloring Formulas for Growing Patterns. Mathematics Teacher 98(7): 472-475.
Resources
Exposure to repeating patterns comes early - often well before students are at school. It is important for young students to explore repeating patterns and to see that patterns continue, sometimes in more than one direction. However, repeating patterns can also be used to start thinking in a more functional way. Simple repeating patterns such as

can initially be used with questions such as:
- What comes next?
- What comes before the first square?
- What are the next three shapes in this pattern?
However, they can also be used to ask questions such as:
- What would the 10th shape look like?
- What would the 21st shape be?
or statements such as:
- Draw the 35th shape.
This type of questioning begins to move students towards developing strategies to look beyond just working out what the next shape will be. It is also the beginning of assigning an ordinal number to each shape, which becomes important later when working out general rules for number patterns. To assist in this process, numbers can be placed underneath the shapes when working out the 10th or 21st shape to start encouraging students to see the relationship between the ordinal position and the shape. If students work out the nth shape by drawing all the shapes in between, ask them to find the 40th or 50th or even 100th shape to encourage them to use a more functional strategy that does not require counting on.
One common misconception when students are working with repeating patterns is that they will often repeat what is given rather than looking at what "chunk" or part of the pattern is actually being repeated. For example, given the pattern

and asked to draw the next shape in this pattern, a student may draw a square because they return to the beginning of the given pattern and repeat it from there. While technically not incorrect, the student should be encouraged to look for the repeating "set" - in this case the square, circle and triangle. These could even be circled or shaded to show which part is the repeating part of the pattern.
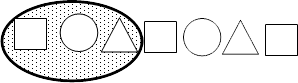
Once students are comfortable identifying the repeating "set" or "chunk" and predicting the nth shape when there is a single variable (e.g. shape), introduce other variables such as shading, size or orientation. Ask students to draw the next three shapes in this pattern, and then draw the 12th shape, 23rd shape etc.

Size and/or orientation, for example, can also be used to create increasingly complex patterns. Students can also create their own repeating patterns.
| Set | Blue | Red | Total |
| 1 | 2 | 1 | 3 |
| 2 | 4 | 2 | 6 |
| 3 | 6 | 3 | 9 |
| 4 | 8 | 4 | 12 |
| ... | ... | ... | ... |
| ... | ... | ... | ... |
Ask students to describe the relationship between the set number, the number of blues and the number of reds and the total number of beads (tiles). Encourage them to look across the table.
The following statements are examples from Year 6 students who carried out this activity:
- Red is half the number of the blue.
- The number of red is 1/3 of the total.
- The number of blue is 2/3 of the total.
- The number of blue is twice the number of red.
One student said "The blue is the 2 times table." This indicates a student who is looking down the table rather than across it. They may be using a recursive strategy to work out what comes next in the pattern.
Next, ask students a series of questions to encourage them to explore the relationship across the table between the set number (ordinal position) and the number of blue and red beads or tiles. Have students explain how they worked out their answers to see if they are using a functional strategy. Examples of questions could be:
- If I have 10 blue beads (tiles), how many red beads (tiles) will I need to make the pattern?
- If I had 48 red beads (tiles), how many blue beads (tiles) would I have?
- If I had 212 blue beads (tiles), how many red beads (tiles) would I have?
- If I have 12 'sets' of beads (tiles), how many blue beads (tiles) would I have? How many red beads (tiles) would I have?
- If I have 30 beads (tiles) in total, how many are blue and how many are red?
If students continue to use a recursive strategy to work out their responses, use larger and larger numbers to encourage them to look more functionally at the pattern. Discuss how a rule could be developed to describe the pattern. For example, students might say that the number of red beads (tiles) is the same as the 'set' number or that the number of blue beads (tiles) is two times the 'set' number or twice as much as the red beads (tiles).
Having explored the pattern in this way, an opportunity now exists to introduce the concept of n. Explain that n represents 'any number'. Ask students to explain their rule in terms of ‘any number’ – for example they could state: "For any number of sets, there will be three lots of red beads." Now have them substitute n for "any number". Record student responses as they are stated e.g. "Triple n" or "n × 2" or "n + n". Clarify that mathematicians usually say 2n rather than n × 2 but accept what students give, modelling the mathematical format where possible. This is also an opportune time to show students that n × 2 is the same as n + n or Triple n and 3n are equal.
Resources
- Patterns and rules II
- Matchstick patterns II
- Calculator patterns
- Missing numbers
- Chain of numbers
- Growing patterns
- Use the rule
- Fish patterns
- Growing leaves
- Pyramid pattern
- Making triangle patterns
- Making triangle patterns II
- Block patterns II
- Stacking cans
- Making triangles
- Patterns and rules III
- Match patterns
- Making stick patterns
- Missing numbers II
- Stick patterns and rules II
- Missing numbers and rules
- Stick patterns and rules
- Continue the patterns
- Continue the shape patterns
- Making stick patterns II
- Making more stick patterns
- Tukutuku patterns
Early number pattern work often focuses on finding the next number in a sequence. Students can use a recursive strategy to work this out. This means that they determine the next number in the pattern based on the previous number. When asked to find the next two numbers in the following sequence: 3, 6, 9, 12, __, __ students will state that the rule is "add 3" and to get the next number they add 3 to 12, giving 15, then another 3 to that answer, giving 18. This strategy can also be called the recurrence relation or the iterative strategy.
Students tend to use the recursive strategy in their pattern work. This way of working out rules for patterns is a powerful strategy that is used in computer programming. However the usefulness of the recursive strategy in the type of pattern work students are likely to encounter in their school years is limited. For example, if asked to find the 20th number in the sequence above, students using a recursive strategy would have to work out all the numbers between the last given number (12) and the 20th number (60).
Resources
- Necklace patterns
- Cross pattern
- Patterns with X and O
- Multiplication rules
- Picking cherries
- Domino towers
- Sides and diagonals
- Cross patterns
- Exercise programme
- Black and white triangle patterns
- Beehive patterns
- Fitness plan
- Number machines II
- Squares and matches
- Diamond patterns II
- Turbine patterns
- Finding the rule for the pattern
- Repeating bead patterns
- Matchstick patterns III
- Diamond patterns
- Matchstick patterns
- Tables and chairs
- Number machines
- Building patterns
- Building patterns II
- Morning coffee
- Grid triangles
- Knitting needles
- Machine rules
- Alien shape patterns
- Machines with rules
- Stick patterns and rules II
- Stick patterns and rules
- Continue the shape patterns
- Making stick patterns II
- Making more stick patterns
- Repeating bead patterns II
- Tukutuku patterns
The New Zealand Curriculum states that, at Level 3, students need to solve problems that "connect members of sequential patterns with their ordinal position…" In other words, students need to develop explicit or functional strategies to work out a rule to ascertain what comes next in a number pattern. Using the example given in the section on recursive (sequential) sequences, to determine the next two numbers in the pattern, students might put the sequence into a table, with the ordinal position of the number in the pattern shown along the top row.
| Ordinal position: | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | nth |
| Number: | 3 | 6 | 9 | 12 | ? | ? | ? | ? |
By exploring the relationship between the ordinal position of the number in the pattern and the number itself, a functional rule can be generated. The number in the pattern is a function of its position. For example, the 4th number in the sequence is 12. 12 is 4 (ordinal position) × 3.
In this case the general rule can be stated as "the position of the number × 3". Pronumerals such as n can be introduced to develop this general rule for the pattern. In this way n can replace “the position of the number” and stand for any number, making the rule n × 3 or 3n. The table can then be completed:
| Ordinal position: | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | nth |
| Number: | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 3n |
Functional strategies and rules are very powerful because they allow the user to work out any number in a pattern without knowing its predecessor. The information and resources developed for this concept map explore some ways in which students can be encouraged to develop functional or explicit strategies in their work with patterns.
There are many ways in which functional relationships can be explored. In our research we started by exploring patterns that could be made from ice block sticks or matchsticks as a way to look at how the construction of a pattern can inform the rule for that pattern.
Initially we used simple patterns with rules such as 2n, 3n or 4n because these were the types of rules we had co-constructed while working with bead patterns. Students used ice block sticks to physically build the patterns, then put their findings into a table and used this information to work out the rule for the pattern. For example, the following "Tent" pattern was used:

Students were asked to construct the pattern using ice block sticks, then make a table and record how many sticks were needed to make each tent pattern. They were then asked to continue the pattern in order to work out what the rule for the nth pattern would be.
Warren and Cooper (2008) conducted research into patterns with 8 to 9 year old students. They made the ordinal position of their patterns visually explicit by placing position cards underneath the pattern, helping to emphasise the link between the pattern and the pattern number. This is demonstrated below with the matchstick pattern “Flats”.
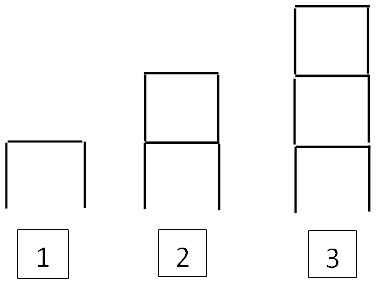
As well as working out how many matchsticks are needed to make a certain pattern number, students can also be asked questions such as “How many tents can I make with 28 matchsticks?” or “How high would a flat be that had 36 matchsticks in it?” In this way students are encouraged to look across their tables from number of matchsticks to pattern number and use their rule in reverse. In our research we did a little of this but our main focus was on getting students to see the pattern and make a general rule for it. When students have got the idea of simple rules such as 2n, 3n, 5n, etc., introduce them to patterns that require both multiplying and adding. Some examples are:
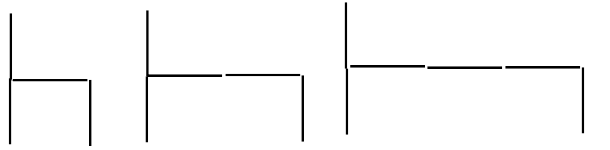

When constructing the trees, for example, each tree has two sticks for the trunk then a certain number of triangles, each made with three matchsticks. Encourage students to see that the number of triangles matches the ordinal number. Placing ordinal cards underneath their constructions could help with this. Students could be asked “What would the 6th pattern look like?” and asked to construct it without making all the patterns in between. Ask the students to explain how they could work out what the 6th or 10th or 25th patterns would look like. At this point a rule explaining that the pattern is “the ordinal number times three plus 2” is a good starting point. From here, students can use n in place of the ordinal number and then this can be used to describe the rule more succinctly as 3n + 2.
Similarly with the beds pattern, the bed “head” and “legs” remain the same throughout and require three sticks in total to construct, while the “base” of the bed increases – the number of sticks needed to make it is the same as the ordinal number of the pattern. Therefore, the pattern is n + 3.
The classic matchstick pattern:
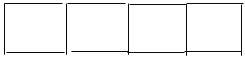
can be used to explore the different ways that the same pattern can be built up and the rule described in apparently different ways. For example, this pattern can be constructed by putting down 1 matchstick

then adding three more each time to construct a set of 4 squares.
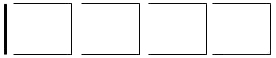
This can be described as: 1 + 3 + 3 + 3 + 3. Another way to construct the pattern is to make the first square:

Then add three matchsticks each time to make the set of 4 squares:
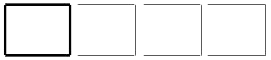
This can be described as: 4 + 3 + 3 + 3. A third way to construct the pattern is to place the 5 vertical matchsticks first:

Then add two rows of 4 matchsticks to construct the set of 4 squares:

This pattern can be described as: 5 + 4 + 4. Although these pattern descriptions may at first appear different, when they are presented as a general rule, it can be seen that they are equivalent.
1 + 3 + 3 + 3 + 3 becomes 1 + (4 × 3) which can be generalised as 1 + (n × 3) = 3n + 1
4 + 3 + 3 + 3 becomes 4 + 3 × 3 which generalises to:
4 + 3(n – 1) = 4 + 3n – 3 = 3n + 1
5 + 4 + 4 generalises to (n + 1) + n + n = n + n + n + 1 = 3n + 1
The most difficult aspect of constructing these rules from the initial description of the pattern is firstly recognising that n is the number of squares (in this case, 4) and then using n to describe other numbers. In other words, understanding that if n is 4, then 5 can be written as n + 1 or 3 is the same as n – 1 can be a difficult concept for students to understand. However, there are opportunities here to explore some algebraic generalisations.
Meeks Roebuck, K. I. (2005). Coloring Formulas for Growing Patterns. Mathematics Teacher 98(7): 472-475.
Stacey, K. and M. Macgregor (1997). Building Foundations for Algebra. Mathematics Teaching in the Middle School 2(4): 252-260.

