Sending envelopes

Sending envelopes

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about using a smaller shape to work out the area of a larger shape.
 
 
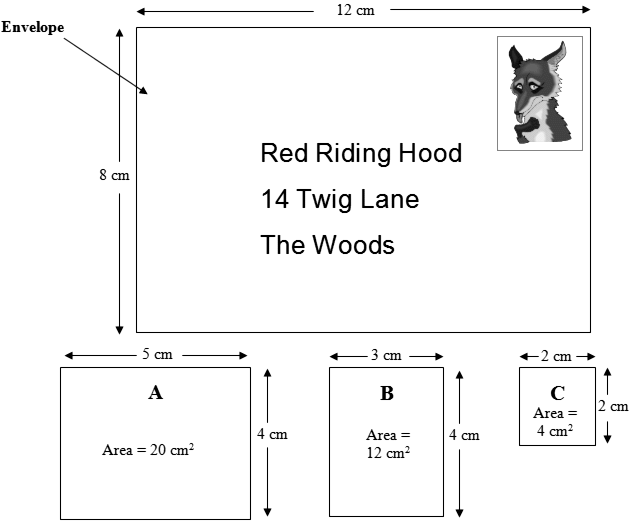
a) Which of the 3 shapes above (A, B, C) would be the best to measure the area of the envelope? (select one)
 


A   /   B   /   C
     
b) Explain your reasons for your choice in a) in the space below.
 
 
 
 
 
 
 
 
c) Show how to work out the area of the envelope.
 

 
 
 
 

 Area: _____
Task administration: 
This task is completed with pencil and paper only.
Level:
4
Curriculum info: 
Maths, Geometry and Measurement, Measurement
Keywords: 
area, units of measure, repeated units, unitising, work samples
Description of task: 
Students select a non-standard unit of measure to measure an envelope and explain their choice.
Curriculum Links: 
This resource can be used as one source of evidence of students' understanding of using side or edge lengths to find the areas of rectangles with whole number dimensions.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Measurement sense, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y8 (10/2010)
a) B
[NOTE: C also could be used, but B is better because it only requires 8 of them to fit to the envelope, whereas C needs 24]		 moderate
b) Any 1 of:
Explanation of using factors for shape B, e.g.,

  • because 3 goes into 12 four times and 4 goes into 8 two times and it would save time than putting 2 into 12 six times [and 2 into 8 four times].
  • because 3 is a factor of 12 and 4 is a factor of 8.
  • because 3 goes into 12 nicely and 4 goes into 8 nicely.
  • I know that 3 × 4 = 12 and 4 × 2 = 8
  • 12÷3 and 8÷4

Explanation of using factors for shape C, e.g.,

  • because 2 goes into both 8 and 12 so C can be replaced over and over again

With no gaps and can fill the envelope. Explanation that shape A does not fit exactly, e.g.,

  • 5 does not divide [into] 12 or 8 so A is useless. Explanation about factors but details not specified, e.g.,
  • You can divide the numbers by the envelope numbers.
 difficult
c) 96
Any 1 of:
Scales up from shape B, e.g.,

  • 4 × 2 = 8 and 3 × 4 = 12 so 8 × 12 [area of B] = 96

Scales up from shape C, e.g.,

  • Using shape C, 12 ÷ 2 = 6 and 8 ÷ 2 = 4; 6 × 4 = 24

Using horizonatal strips, e.g.,

  • 3 fits into 12 four times area of [4 x 12 =] 48; 48 x 2 = 96
  • 12 cm x 2 = 24 cm2; 24 cm2 x 4 = 96 cm2, i.e. vertical strips

Uses the dimension of the envelope but not the shapes, e.g.,

  • 8 × 12 = 96
  • 8 × 12 = 8 × 10 + 8 × 2 = 80 + 16 = 96

Gives a diagram of how the shapes fit the envelope, e.g.,

 difficult
difficult
Teaching and learning: 
This resource tests if students can use the side lengths and the areas of non-unit shapes to deduce the area of larger shapes.
Diagnostic and formative information: 
  Common response Likely misconception
c) 40 or 20 Confuses area and perimeter
a)
b)		 A
Because it is bigger		 The bigger the shape the better
The student can see that the large shape will need to be used fewer times but indicates that they do not recognise that it will not fit the envelope an exact number of times
a)
b)		 A
It is a similar shape		 Choosing similar looking shapes (ignoring factors)
The student uses the visual similarity of the shape and the envelope without checking if the shape will fit the envelope an exact number of times.
a) C Overlooks the most efficient shape
Identifies that shape C is appropriate to use, but does not see that shape B fits in a smaller number of times and is hence easier to scale up with.
Next steps: 
Confuses area and perimeter
The meaning of the words "perimeter" and "area" is a knowledge issue. Students need to see both concepts are valid measures, but they measure different things.

  • Perimeter measures the length of the distance around a shape. This can be counted using unit lengths (counting from one on materials), or by adding the lengths of each side.
  • Area measures the "space" covered on a flat surface. Questions such as "How many stamps of the size of each shape would it take to completely cover the envelope?" may be useful.

The bigger the shape the better OR Choosing similar looking shapes
These students need to develop the concept of factors to base their decisions on. Ask these students if the shape they have chosen (Shape A) could be used to completely cover the envelope. If they cannot answer this or answer it incorrectly, they should make several of the shape, and try covering the envelope with them. The envelope and the shapes need to be redrawn to the actual dimensions given. They can then use repeated addition of the areas of the non-standard shapes to get the total area.

Overlooks the most efficient shape
These students should compare using shape B and shape C. Challenge the students to come up with a strategy that works if they are not allowed to use the formula (length × width) to get area, but can just use the information provided. They should be able to see that shape B needs just 8 replications to cover the envelope (leading to 8 × 12 = number of shapes needed × area of the shape = 96). Here 12 refers to the area of shape B, not the length of the envelope. Shape C needs 24 replications to cover the envelope (leading to 24 × 4 = number of shapes needed × area of the shape = 96).
Students who drew how shape B (or shape C) could fit the envelope 8 (or 24) times had the highest mean ability of all students, e.g.,
These students recognised that it only took 8 of Shape B to fill the envelope, This gives an area of 8 × 12 cm2 = 96 cm2.
While this appears to only meet the Year 6 standard,the student needed more sohisticated multiplicative understanding to recognise the factor relationships implicit in their drawing which meets Year 8 expectations.
The most sophisticated response recognises the multiplicative nature of the non-unit sqaures, i.e., (4 × 2) × 12 cm2 = 96 cm2.