Sliding cubes

This task is about statistical investigations.

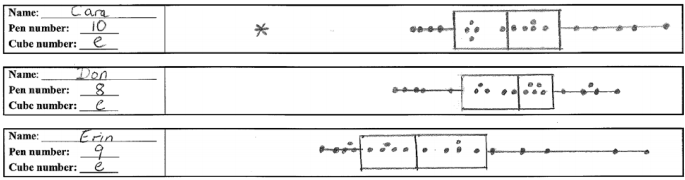
Mrs Judd gets a box of ball-point pens. She wonders if all the pens have equally strong flicks. To test this, she flicks a cube in the centre and measures how far it slides.

Part I - Getting started - whole group

List as many different things as you can that will affect how far a cube will slide when it is flicked by the pen.

Watch the teacher flick the cube several times.

Why does the cube sometimes travel different distances, even though it is flicked in the same way?

Watch the teacher show how to use the recording strip.
Write your name, and details of the pen and cube you used.

Part II - Collecting and looking at data – in pairs My name: ______________________ My partner’s name: _____________________
c)	1. Get one person to flick the cube exactly in the centre. 2. The partner marks the distance travelled with a dot on the person’s recording strip. 3. Return the cube to the person. 4. Repeat this 20 times. 5. Swap roles and repeat steps 1 – 4 so both of you have flicked the cube 20 times each.
d)	Compare the results of your recording strips to decide which person’s cube usually goes further or if both cubes travel about the same distance. i) My cube usually travels: further / about the same distance / not as far (circle one) ii) Explain your answer (make reference to the data plotted on your two recording strips).
Part III - Looking at all the data – whole group Get into larger groups. Each group puts their recording strips on the wall or a large sheet of paper with blue-tack. Make sure each pairs’ strips are one under the other.
e)	Discuss what you notice about your groups’ results. Make your own notes.
f)	i) Do you think that all the pens flick the cubes about the same distance? Yes / No (circle one) ii) Explain your answer (make reference to the data plotted on all the recording strips).

Task administration:

This task is completed with pencil and paper, and other equipment.

Equipment:

For each pair of students:

One dice or wooden cubes approx 1cm³
Write an identification number on each cube;
One ball-point pen with clicking mechanism. Write an identification number on each pen;
Two answer sheets, one for each student;
Two data recording sheets, one for each student;
Blue-tack.

This task can be performed in separate sessions, especially Part III.

I With the whole class

Discuss how the strength of a pen’s spring could be measured by how far it can flick a cube. Get the students to answer a).
Discuss with the class their answers to part a). Agree on a way to flick the cube in a constant way.
Make a spot in the very centre of one face of the cube, and always flick on this, with the pen touching the cube before it is flicked.
Flick the cube two or three times. Stress that you are trying flick it exactly the same way each time. Get the students to answer b).

II With the whole class, then in pairs

Show how to use the recording strip. Emphasise that the recording strip allows students to get lots of data rapidly.
Break into pairs, with each pair having one dice, one pen; and an answer sheet and a recording strip for each partner.
Students need to record their name, and the pen and cube numbers on each recording strip.
Students can have a few practice flicks.
One student should then flick their cube 20 times. The other student places a dot on the recording strip for each flick and returns the cube to the person who is flicking it. This speeds up the process and improves the consistency of results.
Students then swap roles.
Get the students to answer c) and d).

III In groups of about eight (four pairs)

Get each group to display their graphs one under the other. Blue-tack the recording strips to the wall or a large sheet of paper.
Get the groups to discuss what they think their graphs are saying about the strength of the different pens they used.
Get each student to record notes in e), and to answer f).

Using the template

Data Recording Template.pdf

Cut out both pieces of the template and join them together. Double sided adhesive tape works well.
Write your name and the equipment you are using in the description box (or even on the reverse side).
Flick the cube a little below the template strip in line with the “Start line” and record the distance it travelled with a dot. If the cube slides further than the length of your strip, use more strips stapled or glued together.

Flick the cube a total of 20 (or more) times, always starting it in the same position and flicking in an identical way.

The graph in Part 4 can easily be turned into a box-and-whisker graph (box plot). This helps interpret the graph. Draw vertical lines at the median, and the lower and upper quartiles. Join these to make a "box". Draw two horizontal lines ("whiskers") from the quartiles to the maximum and minimum point. The whiskers to be no longer than 1.5 times the length of the box (the inter-quartile range). Other points can be marked as an asterix (*), as something unusual may have happened. We call these points “outliers”.

Notice that there are exactly the same number of dots in each quartile (in this case 5). This always happens when the sample size is a multiple of 4.

Template for recording data - recording strips [pdf]

Level:

Curriculum info:

Maths, Statistics, Statistical investigations

Key Competencies:

Participating and contributing, Relating to others, Thinking, Using language, symbols, and texts

Keywords:

distribution, fair testing, dot plots

Description of task:

Students state what things will affect how far a cube will travel when flicked in the middle with a ball-point pen, and conduct an experiment to see what happens in practice.

Curriculum Links:

This resource can be used to help to identify students' understanding of an statistical investigation.

Plan a statistical investigation: Evidence of students’ ability to identify variables that affect how far the cube travels.

Look for naming four or more things that can influence the distance the cube travels.

Collect data: Evidence of students’ ability to record data accurately.

Look for plotting all 20 data points correctly, distinguishing points that are close together if appropriate.

Analyse and make conclusions: Evidence of students’ ability to compare the distribution of different sets of data.

Look for appropriately identifying that the distributions are similar or different, and explaining their reasons clearly.

Key competencies

This resource involves:

Predicting outcomes of an experiment and Exploring patterns and relationships in data and dealing with uncertainty, which relate to the Key Competency: Thinking
Communicating the findings of an experiment, and explaining variation, which relate to the Key Competency:Using language, symbols and text
Working collaboratively and sharing their work with other students, which relates to the Key Competencies: Relating to Others and Participating and Contributing

For more information, see https://nzcurriculum.tki.org.nz/Key-competencies

Learning Progression Frameworks

This resource can provide evidence of learning associated with

Statistical investigations, set 5

within the Mathematics Learning Progressions Frameworks.

Read more about the Learning Progressions Frameworks.

Answers/responses:


a)	A selection of: • The weight, size or shape of the cube; • The pen that is used / the strength of the spring in different pens; • The smoothness of the surface; • The smoothness of the cube’s face; • The position on the cube that the pen flicks on; • The distance of the pen from the cube; • The way the pen is flicked / way of holding pen; • Other reasonable suggestions. NOTE: The more different valid things a student suggests, the more sophisticated their thinking.
b)	A statement that: Specific conditions varied slightly ("better flick", "hit a different spot") Maybe because you didn’t put the pen exactly where it was before. You might not push it on exactly the same spot. The position of the cube might have been different. You pushed it differently. The conditions changed in some systematic way. Because the spring may have lost some of its strength. Because the surface may have changed with the cubes going across it. [one pair of students numbered their dots. This would allow them to see systematic changes such as a spring gradually losing its strength] Lots of things influence how far it goes. There are many reasons that each cube is hit a little differently in many ways. Because there are so many variables that can’t be controlled without machines. You always get slight differences for no obvious reason. [It is] random.
c)	The strip has 20 dots recorded on it, and the descriptions are filled in.
d)	A statement, consistent with the two sets of points, that gives a holistic description of the dots. [e.g., All pairs in the sample had results that were approximately the same as each other]. We both got ours clumped up in a space and we have quite a lot the same. Well JJs and mine travelled very much the same [distance] with a few measurements further away. They are bunched up [the same way]. Ours varied the same amount. Do not accept one that is solely based on the location of the mean, median, maximum, minimum, mode, or other specific features of the dot plot.
e)	Notes are for the student.
f)	A reasonable explanation that compares the graphs holistically. Answers will depend on what the graphs show. They must have had different weights and different spring strengths. Students may conclude that differences are due to factor other than the different pens, such as using different cubes, different surfaces, etc.

Based on a group of 10 Year 7 and 8 students

Teaching and learning:

This resource involves Statistical investigations in a science context. It uses the Predict, Observe, Explain (POE) strategy.

It also uses the statistical enquiry cycle (PPDAC: Pose - Plan - Data - Analyse - Conclusions - Communicate).

In statistics, the context of the investigation is vital. In this resource, the phenomenon under investigation is scientific. In particular it involves forces and friction acting on a body (the cube or dice).
A key statistical idea is that an experiment must be repeated observations number of times to build up a picture not just of the mean (average) of a measurement, but also how much the data points vary.
The distribution of the data is the overall shape of the graph. This involves looking at where the "biggest clump" of the data is, and how much the data varies.

Diagnostic and formative information:

Further opportunities for statistical assessment or teaching

Creating dot plots (click on the link).

Creating box plots (box-and-whisker graphs) (click on the link).
This is very intuitive if the number of points is divisible by 4, as a quarter of the points lie in each quartile. The box represents where half of the data points lie.
Example:

The point marked as an asterix is unusually short as it is far away from the other dots.

Distinguishing between data sets.
Students can use the box plots to help them distinguish whether two or more sets of points are similar or different. Alternatively they could circle most of the points. The less the boxes (or circles) overlap, the more likely it is that the sets of distances differ.
Example:

Cara and Don’s pens flicked the cubes about the same distance, but Erin’s pen usually flicked the cube shorter distances, even though the data overlaps.

Identifying dependent variables
In this case, the dependent variable is the distance the cube travels. This depends on the pen or dice used, the surface it is on, etc. (the independent variables).

Plotting the data inaccurately

Interprets individual features of the graph (e.g., one maximum is bigger than the other)

None of the students in the sample made these statements, but they are common in other similar resources such as Sliding, spinning, tumbling (ST8109).

Cannot distinguish two data sets that are somewhat separated

Observes that all the dots are in one of the same general part of the recording strip, even when some are clustered into different locations. Every graph shows the most flicks around the same area. [When some clearly differ] Most of the dots are in the middle piece. [Each students strips were in three joined sections]

Next steps:

Plotting the data inaccurately
Students need to have a systematic way of accurately recording their data. It is best to observe them, and to then prompt them to be more consistent and accurate.

Interprets individual features of the graph

Students need to look at the data holistically rather than focusing on specific features. Ask the students to put a circle around where most of the points are. They could also draw a box plot and compare the location of the box with the points they have circled.

Cannot distinguish two data sets that are reasonably well separated
Students may need to look at the graphs more closely. This can be aided by asking the students to put a circle around where most of the points are (i.e., the “biggest clump”). They could also draw a box plot and compare the location of the box and the “clump” of points they have circled. The students can then see if the circled points or boxes are all in about the same position, or differ. It may well be that several sets of data are similar, but some are different.

Get the students to listen to other students’ ideas, especially those who spot two or more data sets that are quite different. This is a difficult skill, but exposure to many situations of this sort will help students to develop an informal feel for when data sets differ.

You are here

Resource user links

Sliding cubes

Sliding cubes