View from a different angle II
| Y8 (10/2009) | ||
|
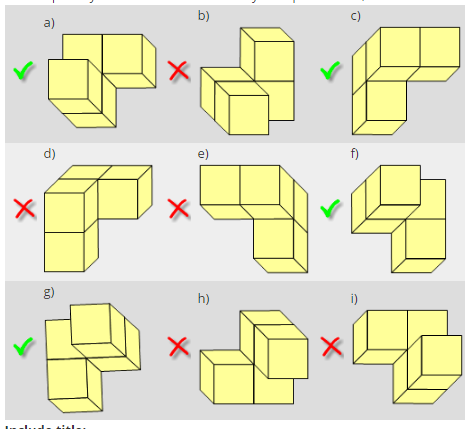
a) |
True 9 correct 8 or more correct* |
very easy
difficult |
NOTE:
*Students who get 8 correct but get e) incorrect (i.e. they circle it) should not receive partial credit. This is because they do not distinguish that shape c) and shape e) are mirror images so only one of them can be correct.Students who got only 7 shapes correct had a mean ability no higher than students who got 6 or fewer correct, and so were not given partial credit.
- This resource is about being able to visualise in three dimensions by recognising which objects are identical with a given one. The objects that are not identical to the given one are mirror images of it.
- Students find each individual shape easy or very easy, but only a minority can get all nine shapes correct. Only those who got 8 or more correct have higher mean ability than those who got fewer correct.
- Shape c) was the hardest to get correct, followed by d), g), b), and e). All of these except c) are not identical with the original shape.
- f) was the easiest to get correct followed by a), h), and i). All of these except i) are identical with the original shape and should have been circled.
It was therefore more common for students to see mirror images as identical to the original, but less common to think that an identical shape was different.
| Common response | Likely errors in visualisation |
| Circles shapes that are not identical to the original, or Circles all shapes. | Sees mirror images as identical to the original shape |
| Does not circle a), f) or h) |
Does not recognise identical shapes This was less common than the above misconception. |
|
Does not circle c) or Does not circle c) and circles e) [i.e. transposes responses for c) and e)]. |
Has issues with one specific shape (c) Shape c) is the most difficult. This may be that it is hardest to see how to superimpose this particular orientation onto the original shape. A number of students with higher mean ability made these two errors. |
The 2-dimensional representation of shapes c) and e) are clearly mirror images in a vertical mirror, so both being circled indicates a lack of higher level geometric visualisation. The same would be the case for the pairs a) & i), and f) & g). Ironically, this mirror image relationship between the original shape and shape b) does not make getting b) correct easier.
These students most probably need to build the models with physical blocks to persuade themselves that the shapes are not all identical, but fall into two groups that are mirror images of each other. Soma cubes have shapes like this that can be used.
Soma cubes
These have two shapes like this that can be used. The two mirror-image shapes are shown here. Students will find that they cannot be superimposed on each other by twisting or moving them. One spirals in a clockwise direction, and the other anticlockwise.
"Right screw tetracube".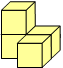 |
"Left screw tetracube".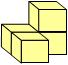 |
 Like the left hand |
 Like the right hand |
They are similar to the diagrams of the two hands, although the terminology is a little inconsistent. Notice how easy it is to see the relationship between the shapes when the mirror line is vertical, and the shapes are side by side. Mirror-images of the other shapes in the Soma cube are not distinct from each other, but can be superimposed on each other by rotation.

