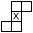Net of an open box

Net of an open box

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about identifying nets for an open box shape.

Here is a box without a top. 

Seven nets are shown below.  Some can be folded to make the box above and some cannot. For each net

1. Circle the net if it can be folded to make the box above.
2. Mark the square that will be the bottom of the box with an X.

The first one has been done for you.

Example:

a) b)
       
c) d)
       
e) f)
Task administration: 
This task can be completed with pencil and paper.
Level:
4
Curriculum info: 
Maths, Geometry and Measurement, Shape
Keywords: 
nets, cubes, visualising
Description of task: 
Students identify which nets can be folded to make an open box shape.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Geometric thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y8 (10/2009)
a)

Yes  

 easy
b) No    very easy
c) Yes   easy
d) No    very easy
e) Yes   easy
f) Yes   

difficult
Based on a representative sample of 155 Year 8 students.

NOTE:
All 6 shapes correct – very difficult
5 shapes correct – moderate.

Teaching and learning: 

This resource assesses students' ability to visualize a 3-dimensional open top cube from a range of nets.  Indicating on the net where the base of the shape is shows that they have an understanding of how the net folds.

Diagnostic and formative information: 

Percentage of students who did not identify nets that can fold into the shape
13% of students did not show that   in question a) could be folded into an open top cube.

21% of students did not show that  in question c) could be folded into an open top cube.

24% of students did not show that  in question e) could be folded into an open top cube.

47% of students did not show that  in question f) could be folded into an open top cube.

The above errors relate to students' ability to translate a 2-dimensional net into a three dimensional shape.  Many nets tend to have the base at the centre of the shape. Question f) had the base at the end of the shape which made it more difficult and required some visual folding and turning to identify firstly that it folded into the shape and secondly where the base was.

  Common error Likely misconception
c)

f)

 Puts cross in a square that cannot be the base when folded.
This misconception is about not being able to completely (and in detail) visualise how the net can fold into the shape.
Next steps: 
A small number of students only identified one shape. This may relate to a reading error and have been because they were only looking for one.  For these students ask them if there are any more shapes that can be folded into an open cube.  Nets can be enlarged and cut out for students to explore how they fold – remind them that the top is open (it is not a total cube).

For students who identified some (but not all the shapes), in a small group ask them how many shapes they (as a group) think there are that can fold into the shape.  Get them to justify how each can or cannot fold.  If appropriate, let them know there are four shapes that can fold. Get students to design several similar nets and have them ask the group to identify whether they can or cannot fold into the shape (or another shape).

For students who identified the shapes, but not the base, or who identified an incorrect base, have them share their findings in a small group and discuss how they can check whether the net folds.  Have students describe how the net is folded and then discuss an easy way to identify how they fold (i.e., having a cross at the base makes it easy to see/visualise). Showing an X provides a reference point that illustrates how the net folds not just whether it folds into the shape. Have them design their own nets for other prisms and have them ask the group to identify whether the nets can or cannot fold into the prisms, or what shape they fold into.