Balance pans

Balance pans

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about writing balanced statements.
a)
In each diagram below, draw in blocks on the right-hand pan to make the scales balance. 
The blocks all weigh the same.
 
  i)
 
  ii)
 
  iii)
 
       
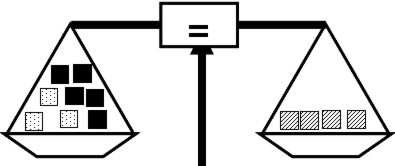b)
For each balance pan diagram below, write an equation to show that the sides are equal. 
For example: 2 + 2 = 3 + 1.
 
  i)
 
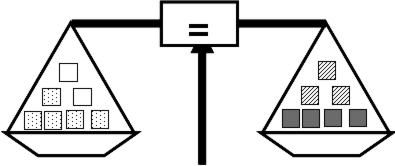  ii)
 
  iii)
 
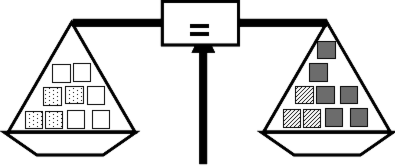  iv)
 
Task administration: 
This task is completed with pencil and paper only.
Level:
2
Curriculum info: 
Maths, Number and Algebra, Equations and expressions
Keywords: 
equality, number sentences, equivalence
Description of task: 
Students draw in the correct number of blocks needed to balance some scales and write equations for scales that show balance.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Using symbols and expressions to think mathematically, set 3
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
a) i)
ii)
iii)		 4 blocks
3 blocks
4 blocks		 1 mark (for all 3 correct)
b) i)
ii)
iii)
iv)		 5 + 2 = 3 + 4
4 + 4 = 5 + 3
4 + 5 = 3 + 6
3 + 7 = 1 + 9		 2 marks (for all 4 correct)
or
1 mark (for 2-3 correct)

NOTE: The order of the numbers on each side of the equation may be reversed.

Diagnostic and formative information: 

Students in our classroom research had little difficulty with question a). As a follow-up, students were asked to write number sentences to represent what was shown on the balance scales. Some common responses to this are presented below.

    Common response Likely misconception
a) i)
ii)
iii)		 6 = 3 + 3, 6 = 5 + 1
9 = 6 + 3, 8 + 1 = 1 + 8
8 = 4 + 4, 8 = 8		 Although correct, these equations do not represent exactly what was shown in the diagrams.
b) i)
ii)
iii)		 5 + 2 + 3 + 4 = 14
4 + 4 + 5 + 3 = 16
5 + 4 + 6 + 3 = 18
7 + 3 + 9 + 1 = 20		 The equals sign is ignored and all available numbers are added together. Seeks to gain closure by 'solving' an arithmetical problem.
Does not see that the equals sign shows equivalence of sides.

Based on classroom-based (Year 4) research on algebraic thinking, December 2005.

Students who gave these responses were comfortable with the idea that equality means that the expression on the left-hand side of the equals sign represents the same quantity as the expression on the right-hand side of the equals sign. They felt comfortable positioning the equals sign at the beginning of a number sentence. However, some were not as comfortable with the idea of having more than one number on each side of the equals sign and gave responses that indicated a need for closure. Responses that did have more than one number on either side of the equals sign did not reflect the actual number of differently shaded blocks presented in the balance pans.

Next steps: 
Students who have difficulty visualising the balance pans from the diagrams provided may benefit from having a real set of balance pans to work with. In our research we demonstrated the concept of equality to the whole class using a set of balance pans and coloured multiblocks, prior to students completing the worksheets. If access to a set of balance pans is limited, students can simply use multiblocks, counters, or other equipment to visually represent the blocks drawn in the diagrams. An alternative to balance pans is to use a coat hanger with string bags tied to each end and small cans of baked beans and spaghetti instead of blocks. (Adapted from an idea presented by Marj Horne at the 2006 Numeracy Hui, Auckland, New Zealand.

For students who do not understand what equality means, a discussion about the meaning of the equals sign is a starting point in coming to understand this concept.  Resource What is equal? uses true/false number sentences to generate discussion about the meaning of the equals sign.

It is important for students to realise that the equals sign does not always come towards the end of a number sentence. Once students are comfortable with the notion of equality as comparing the expressions on each side of the equals sign, have them generate their own examples of number sentences that are in a form other than a + b = c, e.g., 7 = 1 + 6 or 8 + 2 = 5 + 5. Cuisenaire number sentences is a practical resource that can be used to practise representing numbers in alternative forms and to reinforce the idea of equality. 
For further information and examples of student generated number sentences, refer to the Algebraic thinking concept map.

Students who ignore the equals sign and/or are only able to generate number sentences in the form a + b = c are often seeking closure – they see a number sentence as a problem that requires solving rather than a representation of a situation.  The idea of closure is explored in the Algebraic thinking concept map.

Students can create their own balance pan problems. A page of blank balance scales has been provided for this purpose.

Once students have grasped the idea of equality using practical equipment or diagrams that visually represent the idea of equality as balance, they can then move on to open number sentences, such as those in resource Equal number sentences.

Click on the link for the Algebraic thinking concept map
 
Figure It Out
What Goes Where? (Algebra, L2-3, page 20 Activity 1).
Coin Control (Algebra, L2-3, page 21) – alternative ways of writing number sentences.
See-saw Numbers (Algebra, L3, page 19).
 
Numeracy Links
Part a) involves recalling addition basic facts and part b) involves students recording written equations (The Number Framework – Knowledge, Stage 4). Equality as balance: refer to A Balancing Act (Book 5: Teaching Addition, Subtraction, and Place Value, page 40) and The Equals Sign Again (Book 8: Teaching Number Sense and Algebraic Thinking, page 12).
 
Other links
The American National Council of Teachers (ANCT) has a computer simulation of the equation as a pan balance These can be downloaded for use with students. https://illuminations.nctm.org/