Shapes that tessellate

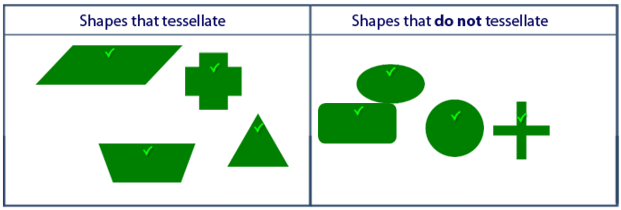
This task is about identifying if some different shapes will tessellate.

A shape that tessellates can fit together to cover a surface without any gaps.

For example the following pattern show the tessellation of an arrow shape.

Question Change answer

Put the eight shapes into the correct columns of the table.

Teaching and learning:

A tessellation of a flat surface can be described as tiling of one or more geometric shapes (often regular polygons) placed edge-to-edge, with no gaps or overlap, that cover a 2-dimensional plane.

Tessellations can provide an opportunity for students to physically explore and solve spatial problems by fitting shapes together. The benefits of this in a teaching and learning environment are that students are able to physically manipulate shapes to solve the problem. Furthermore, by fitting shapes together, the properties (i.e., the length of the sides and the size of the angles at the corners) of the component shapes become more apparent.

Diagnostic and formative information:

Tessellating shapes results

There was no one particular shape that all students correctly noted as tessellating or non-tessellating.

However, the most correctly identified shapes were the circle and the oval (not tessellating) and the triangle, parallelogram and the fat cross (all tessellating). It was surprising that students recognised that the fat cross tessellated, as it is a more challenging visual decision. Also surprising, was the number of students who identified that the triangle did not tessellate.

The two most "difficult" shapes were the skinny cross and the rounded-corner rectangle. The skinny cross being harder to visualise and the rounded-corner rectangle almost looking like a rectangle (which would clearly tessellate).

Explanations (and how many correct shapes categorised)

Explanation involves details of a property:

If the shape is rounded it will leave space. Or if the shape is quite skinny it will also leave space and will not make a pattern. (8)
... rounded shapes don't tessellate (8)

Explanation relates to the definition of tessellation:

It is because it has to have no holes if the shape is tessellated (8)
The shapes look like it. Can cover up a floor (6)
So it can touch and be put together (6)
Because if u put them on the floor and it covers up the whole floor it is tessellated but if u put if u put 1 tipe of a shape but lots of them on the floor and it doesn't cover up the whole floor it is not tessellated (6)
they would fit together (8)
they connected (8)

Explanation is a description of a general strategy:

You look at each shape and see if you can find out if it tessellated or not (7)
I drew a picture in my head (5)
in my head and also using shapes around me (7)
if they can join and turn and flip rotate (6)
by testing it (7)
because i was pituring it. (5)

Explanation is more of an overall observation:

The tessellated shape is like 3-D (4)

Next steps:

Students who could not identify at least 6 out of the 8 shapes may need to explore tessellations by using physical shapes to create a tessellating tiling pattern. This should help to develop the sense of how the tiles fit, but do not overlap. Students could use plastic shapes or cut out paper copies of triangles (equilateral, right angled), squares, rectangles, hexagons, and pentagons, etc. For example, the ARB resources: Making tessellating patterns and Making tessellations provide opportunity for students to construct tessellating patterns. Through this students should start to look at on the properties/attributes of shapes, and ultimately identify that properties such as:

connecting corners need to add up to full rotation,
rounded corners don't tessellate, and
more complex shapes with different lengths that do not join togther without overlap (e.g., skinny cross, as opposed to the fat cross) may indicate non-tessellating shapes.

Students who identified 6-7 of the 8 shapes or provided a general strategy could check over their answers and share their reasoning with other students about why shapes tessellate or not. They could identify specific details about properties of the shapes such as rounded corners, fitting along a line, and identify when gaps between non-tessellating shapes. They could also explore an online (java) animation: http://nlvm.usu.edu/en/nav/frames_asid_163_g_1_t_3.html to develop a sense of tesselltating patterns.

Students who incorrectly identified that the rounded-corner rectangle tessellated could cut and explore, and talk about the corners where they join: what is there? If it is a gap then it doesn't tessellate. Students who incorrectly identified the skinny cross or the fat cross may need to cut shapes out to check for any "gaps". NOTE: cutting and testing would obviously work for most shapes, this should be preceded by student discussion about the completeness of the tiling which is key to whether a shape tessellates or not.

Students who identified all 8 shapes and provided some details about properties of shapes

Have these students develop their explanation to justify using examples. They could work with other students to check each others' justification, and see how they might be able to describe a more general conjecture about why a shape might tessellate or not. Possibly, these students could start to identify the connecting corners of shapes and how the angles need to be a full turn (360 degrees). For example at the connecting corners of an equilateral triangle tessellation pattern where 6 triangles come together, the sum of all 6 corners must be a full turn 360 degrees, and therefore each internal angle at the corner is 60 degrees.

Students may also need to work with other students to develop a more "sufficient" explanation of how to know what shapes tessellate.

A summary of what makes an explanation sufficient could be:

specific details;
appropriate use of examples;
justification;
clarity to another reader (check with a buddy).

Click on the link to the learning intention guide for further information about writing an explanation

Click on the link for an animation (needs Java) from the National Library of Virtual manipulatives to explore tessellations.

http://nlvm.usu.edu/en/nav/frames_asid_163_g_1_t_3.html

You are here

Resource user links

Shapes that tessellate

Shapes that tessellate

Question Change answer

Question 1Change answer