Component:
Introduction
Geometry can be described as the study of spatial relationships involving properties of shape, space, and position. Geometry is an area of mathematics that can provide opportunities to develop accessible creative problem solving and reasoning skills for students. Geometric thinking is concerned with how people reason using the properties of geometric figures and spatial relationships. A key idea in geometric thinking is the idea of spatial sense: just as students can develop number sense, spatial sense is about how students make sense of shapes and the spatial relationships between them.
At the primary and intermediate level, a key purpose of learning Geometry is to build a foundation of spatial exploration; geometric vocabulary; an ability to discuss, explain, and reason. As well as, develop an understanding of geometric relationships to prepare them for the more formal deductive geometry that can follow at high school.
The progression of geometric understanding from primary-intermediate levels could be described as moving from purely visual appearance, through to identifying and classifying the properties of shapes, to deductive reasoning using knowledge of a range of geometric properties.
This concept map is structured around key learning areas of Geometry, many of which link to a range of assessment resources.
Resources
- Reflecting figures
- Star symmetry
- Reflecting the number 5
- Reflection, rotation or translation
- Combining triangle reflections
- Matching shapes and transformations
- Reflecting shapes
- Rotated patterns
- Cutting triangles
- How many times?
- Some kind of transformation
- Still looks the same
- Transforming frogs
- Transforming patterns IV
- How much of a full turn?
- Reflecting on words
- Drawing lines of symmetry
- Reflecting on words II
- Turning the shape
- Reflecting triangle points
- Vector translations
- Rotating rectangles
- Translating points III
- Translating points II
- Translating points
- Finding the angle of rotation
- Transformation or not?
- Tessellating patterns
- Transforming patterns III
- Figure the pattern
- Enlarging shapes II
- Rotating shapes
- Reflecting shapes II
- Transforming patterns
- Cut and turn
- Turning shapes around
- Transforming traffic lights
- Reflecting shapes III
- Showing transformations
- Turning wheels
- Reflecting a clock face
- Reflecting words III
- Transforming Patterns II
- Animal transformations
- Slide, flip or turn animals
- Cat transformations
- Transformation properties
Transformation
Transformation is a key learning component of Geometry, and one of the five achievment objectives of the Geometry and Measurement strand (NZC). Like the properties of shapes in the Shape achievment objective, transformation involves students’ sense of shape and space, but also involves application of a transformation upon that shape or space. Transformations can also connect with recognising and constructing repeating spatial patterns in Algebra (Patterns and relationships), as well as rotation in Position and orientation.
The key learning ideas of transformations (and the Transformation AO) are:
- rotation (turn),
- reflection (flip),
- translation (slide),
- enlargement (and reduction) - sometimes called resizing,
There are also a number of related learning ideas including: scale factor, symmetry (linear and rotational), and invariance (at Level 4).
Like properties of shapes, transformations utilise students' ability to visualise and describe; in this case an identification, description or prediction of a transformation upon a shape or within a geometric spatial pattern.
Vocabulary is important, as students need to know what each type of transformation means in order to apply it to related geometric definitions or situations.
For example, students need to know what each transformation means in order to know whether shapes are congruent or similar:
- shapes are called congruent if one shape can map onto another using only reflection, translation, and/or rotation.
- shapes are called similar if one shape needs to be enlarged (resized) after mapping onto another using reflection, translation, and/or rotation.
Resources
- Parts of shapes
- Puzzling shapes
- How many faces?
- Puzzling shapes II
- Puzzling shapes III
- Corners, faces and edges
- Tangram shapes
- Describing shapes
- Projecting shapes
- Clay shapes
- Without looking
- Parallel lines
- Corners, faces and edges II
- Corners, faces and edges III
- Whetu's frame
- Logical geometry
- Sorting some shapes
- Corners and sides
- Everyday objects
- Describing 2-D shapes
- Describing 3-D shapes
- Shapes that tessellate
- Corners and sides II
- Triangle or not?
- What Shape am I?
- Square or not?
- Rectangle or not?
- Sorting shapes II
- Look at the shapes
- Using a quadrilateral key diagram
Properties and classification of shapes
Properties of shapes is a key understanding for primary and intermediate students to develop. It is also a key element of van Hieles’ analysis stages and underlies much of the problem solving for the Shape achievement objective (NZC), as well as being fundamental to students progressing on to geometric classification and proof in secondary school. The two key interrelated components are: Shape properties and Using shape properties to classify shapes (with justification). Through these experiences students develop and refine conjecture, generalisations, and then definitions (or rules) for shape names and shape classification.
Geometric vocabulary also becomes important, as students require more precise vocabulary to explain or justify their ideas or provide definitions. This becomes especially acute when students are explaining the classification of shapes.
Some of the key vocabulary that students may need to develop in the early years of geometry might be: sides, corners, open/closed shapes, right-angle, parallel, perpendicular, straight, curved, centre, faces, edges, vertex, point, line, plane, solid, dimensions, polygon, quadriliateral, regular, congruent, similar, irregular, concave, convex, etc.
Also important are the shape properties that are required for complete definitions of shapes, e.g., how many properties might be required to give a robust definition of a square? the number of sides and corners, the size of sides and corners, etc.
Ideally, students in their early years transition from recognising and describing 3-dimensional (3-D) objects to recognising and describing 2-dimensional (2-D) shapes. This is because 3-D shapes exist in the real world, whereas fully 2-D shapes exist only in an abstract sense. Students also begin to move beyond simply recognising and naming a shape based only on its holistic appearance or a limited representation of that shape (called a visual prototype):
Holistic appearance is when students describe a shape as like an object they are familiar with, rather than properties of that shape, e.g., "being like a kite/diamond" rather than a shape with 4 equal sides, 4 right angled corners, and a tilted square.
The idea of a "visual prototype" relates to students describing (and recognising) a shape based upon a limited representation, rather than the properties that make up that shape.
For example, if students, very early on, only experience triangles that look like  , this becomes an icon (or visual prototype) for a triangle, and shapes such as
, this becomes an icon (or visual prototype) for a triangle, and shapes such as  and
and  will not be identified as triangles.
will not be identified as triangles.
 , this becomes an icon (or visual prototype) for a triangle, and shapes such as
, this becomes an icon (or visual prototype) for a triangle, and shapes such as  and
and  will not be identified as triangles.
will not be identified as triangles.
Another example, a tilted square could be described as "not a square", because it is not like a square that has always been represented to the student.
Learning experiences with only a limited representation of shapes can reinforce students misconceptions about what defines particular shapes/objects and how they are classified. Conversely, broadening students learning experiences and having opportunities to discuss and justify their ideas with a range of "different" or "strange" objects/shapes can help to direct their focus on the properties of shapes/objects, and then to classification.
Once students can start to decribe and define shapes, they can start to reflect on what properties are necessary and sufficient to define them (Informal deductive/Abstraction level). From here they can begin to use the definitions to develop deductive proofs (Deduction level, van Hiele).
Classification
Classification is about developing a system of naming objects or shapes based on their properties. The initial classification would be whether they are “plane” (2-dimensional) shapes or “solid” (3-dimensional) objects. Other forms of classification include open or closed shapes, straight sides (or not), regular or irregular shapes, convex or concave, and whether the shape is a polygon, and then a regular polygon. Most 2-dimensional shapes that students experience in school are simple polygons, and many are regular polygons. Common examples of regular polygons are: triangle, quadrilateral (square, rhombus etc), pentagon, hexagon, heptagon, and octagon. Note: a circle is not usually classified as a polygon as it has a curved side.
Students should be asked to classify objects and shapes from very early on. Creating their own system of classification is an important first step to understanding properties as well as classes of shapes. Learning experiences around classifying shapes or objects involve students sorting shapes and justifying their reasons, and beginning to build up their understanding of how the names (and classes) of shapes are determined (from the properties of the shapes).
Resources
Tessellation and tangrams
Tessellations and tangrams provide an opportunity for students to physically explore and solve spatial problems by fitting shapes together. The benefits of this are that students are able to manipulate physical objects to solve the problem, and that by fitting things together the properties (i.e., the length of the sides and the size of the corners) of the component shapes become more explicit. This can be further expanded on when students are asked to explain, justify and begin to speculate about which shapes can “fit” together and why.
Tessellations
A tessellation of a flat surface can be described as tiling of one or more geometric shapes (often regular polygons) placed edge-to-edge, with no gaps or overlap, that cover a 2-dimensional plane.
Tessellations that utilise only one geometric shape are said to be regular tessellations; furthermore, the geometric shape is said to "tessellate".
For example: a regular tessellation of triangles (equilateral)

Tessellations that utilise more than one geometric shape are said to be semi-regular tessellations.
For example: a semi-regular tessellation of octagons and squares

Click on the link for an animation from the National Library of Virtual manipulatives to explore tessellations. (needs Java enabled in browser)
Tangrams
Like tessellations, tangrams draw attention to the properties of the shape being used (e.g., matching the length of sides, or complementary angles or offsetting the length of sides to fit in a semi regular tessellation). These all provide an accessible problem solving focus on the properties of the shapes rather than the overall appearance of the shape. Accordingly, this supports students to develop a more “analytical” geometrical understanding involving the properties of shapes.
Tangrams also offer an opportunity to explore a wide range of permutations of how shapes can be combined - again students implicitly rotate and translate (effectively, move) - but not reflect shapes to make the new composite tangram.
Resources
Trigonometry and pythagoras
Pythagoras' theorem and trigonometry
Both Pythagoras' theorem and trigonometry involve solving for unknown quantities of right-angled triangles (or right triangle) by calculating with the other known quantities. For Pythagoras' theorem only the sides are utilised, and for trigonometry sides and angles are utilised. Both Pythagoras' theorem and trigonometry are explicitly mentioned at Level 6 of the New Zealand Curriculum 2007 (Geometry and Measurement, Shape). In the previous curriculum (NZC, 1992) they were evident at Level 5.
Pythgoras' theorem
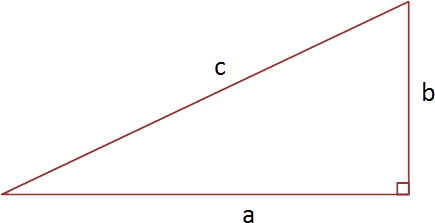
Pythgoras' theorem describes the relationship between the three sides of a right-angled triangle. The theorem states that the square of the length of the hypotenuse is equal to the the sum of the length of the other two sides of the triangle. The hypotenuse is defined as the side of a right-angled triangle that is opposite the right angle. It is also the longest side of a right angled triangle.
Pythagoras' theorem can also described by the formula:
a2 + b2 = c2
where c is the length of the hypotenuse, and a and b are the the lengths of the other two sides of the right-angled triangle.
Trigonometry
Trigonometry is a component of Geometry that involves utilising the relationship between side lengths and the angles of a right-angled triangle.
It is based upon the relationship between the sine, cosine, and the tangent of a circle.
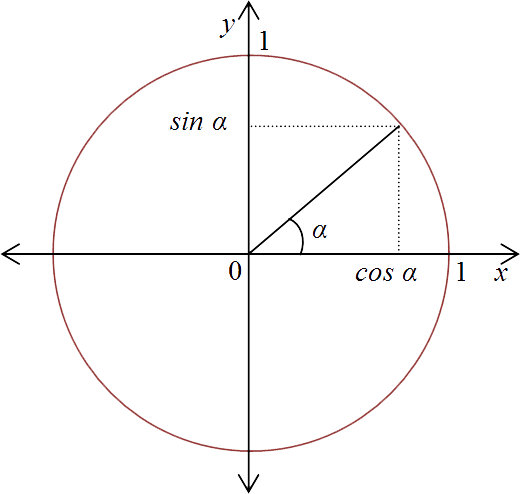
Read more about the trigonometric functions (wikipedia)
Trigonometry forms the basis for surveying, through measuring and calculating distance and bearing given other measures.
Amongst many other trigonometric functions (or ratios), the three common functions are defined below.
Sine (ratio of the side opposite to the hypotenuse)
Sin θ = opposite/hypotenuse
Cosine (ratio of the side adjacent to the hypotenuse)
Cos θ = adjacent/hypotenuse
Tangent (ratio of the side opposite to the side adjacent)
Tan θ = opposite/adjacent
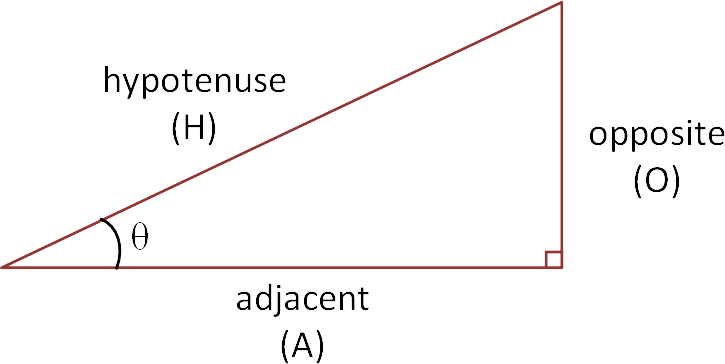
The mnemoic, SOH CAH TOA, can be used to help students remember the definitions of the three trigonometric functions above. Note that the opposite and adjacent sides are dependent upon which angle is involved in the calculation. For example, in the diagram above, the labels are appropriate for the angle θ, if the angle involved was the top right angle, the opposite and adjacent labels would be swapped.
These trigonometric ratios can be used to find any given side or angle in a right-angled triangle. They can also be used to derive further trigonometric ratios.
Position and orientation
van Hiele levels of Geometric understanding
The van Hiele model of geometric understanding is a commonly referenced model that underlies much contemporary research and curricula. It describes a hierarchy of geometric understanding at several sequential levels. These levels depend upon instruction and understanding, rather than age/maturity, and students progress through them in order. Over time there have been a number of suggestions for modification. Two notable adjustments are: a “pre-cognitive” level (Level 0) and some kind of Level 1+.
Pre-cognitive Level (0)
Students cannot identify a common class of shape reliably. Students at this level may correctly identify some, but not all of the common types of shapes: triangle, circle, square, rectangle/oblong.
Visual Level (1) [also called Level 0: Visualisation, van Hiele]
This level is where students recognise a shape based on its overall appearance (called visual prototype), rather than by the properties that make it up. They may well be able to sort shapes based on this “holistic” recognition, but shapes are like icons. For example, many squares simply look like a standardised representation of a square - however, if it was rotated 45°, students may not recognise it as a square and try to describe it as a “kite” or “diamond”. Similarly, an upside down triangle or a very long extended triangle may not be considered a triangle because it does not look like a common representation of a triangle, e.g., an equilateral triangle. Students may also describe a shape in terms of an object that it looks like rather than by its geometric name.
Visual Level (1+)
Students recognise a single property of a shape. At this level students can start to see that a shape has properties that determine what type of shape it is. For example they may say a square has four sides, and a triangle has three sides. "Sides" are only one of a number of properties that can be used to describe shapes. Once students begin to identify more than a single property they are exhibiting the next level of understanding (Descriptive/Analysis level).
Descriptive/Analysis level (2) [also called Level 1: Analysis, van Hiele]
This level is where students can identify and describe more than one property of given shapes. Geometric vocabulary becomes more important in conveying these developing interrelated ideas. For example, students may be able to identify the properties that make up a triangle: closed shape (or polygon), 3 straight sides, and 3 corners, and, furthermore, that the sides or angles do not have to be equivalent.
Informal deductive/relationship level (3) [also called Level 2: Abstraction, van Hiele]
At this level children can identify and discuss the relationships between the properties of different shapes and different classes of shapes and can develop logical arguments about the name or class of a shape using some properties of that shape. For example they may know that all rectangles have 4 right angle corners and 4 straight sides, and therefore a square is a type of rectangle, but not all rectangles are squares. Another example may be that all quadrilaterals have 4 sides, therefore all rectangles are quadrilaterals. Definitions given for shapes are sufficient and concise.
The other two levels of van Hieles’ geometric understanding are: Formal deductive level (4), where students can construct proofs using definitions and axioms; and the Rigor level (5), where students can work with abstract mathematical systems, with axioms, corollaries, and theorems. These are generally exhibited by students working at Level 5 or above of the New Zealand Curriculum.
Read more about the van Hiele's theory of Geometric learning (Note: the numbers shown for the levels will be different, i.e., Level 0: Visualisation, Level 1: Analysis, Level 2: Abstraction, Level 3: Deduction and Level 4: Rigor).
points, lines and planes
Resources
- Different views
- Different views II
- Make and sketch
- Making a shape
- Making a pyramid
- Isometric views
- Bird's eye view
- Different views III
- Isometric block tower
- Drawing 3-D shapes
- Drawing block towers
- Drawing isometric shapes
- Drawing isometric block towers
- Making a block tower
- Constructing Ziggurats
- Different views IV
- Isometric sketches
- View from a different angle II
- View from a different angle
Connecting 2-D and 3-D with nets, models and views
Geometry and the NZC (Including National Standards)
Geometry in the New Zealand Curriculum is described as the objectives Shape, Position and orientation, and Transformation.
The NZC Shape AO identifies working with (3-dimensional) objects at Level 1 before looking at plane shapes. The Transformation AO, however utilises 2-dimensional plane shapes. At level 1 student learning experiences involve sorting objects by their appearance with a reason for their grouping/classification. They can represent simple transformations (of 2-dimensional shapes), and identify personal locations and work with simple directions for distances and turns.
The subsequent year levels in the NZC address the recognition of shape properties and classification of shapes and objects, and some conjecture and generalisations about how shapes are classified. They look at using maps (including grid references), and applying and predicting transformations. At Level 4 it includes using invariant properties under transformation.
Levels and 5 and 6 involves using pythagoras theorem, and trigonometric ratios in two dimensions, knowledge of geometric properties, and deductive proof to solve geometric problems. Students also construct angles and shapes using instruments (such as compass, protractor, etc).
The National Standards have a similar progressions to the NZC, but differ slightly in that 2-dimensional shapes are introduced earlier, there is some earlier emphasis about identifying a range of features, and justification is made more explicit earlier., and that bearings are also indicated earlier (in Year 8 as opposed to Level 5 of the NZC).
Promotional Text:
Jonathan Fisher, 2015

