Rectangle or not?
0
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about identifying whether shapes are rectangles and what makes them rectangles.
Some children are talking about whether some shapes are rectangles or not.
Task administration:
This task can be completed with pencil and paper or online (with some auto marking).
Level:
3
Curriculum info:
Keywords:
Description of task:
Students decide whether shapes rectangles or not and explain their reasoning.
Curriculum Links:
This resource can help to identify students' understanding of shape properties with justification.
Learning Progression Frameworks
This resource can provide evidence of learning associated with within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.Answers/responses:
| Y6 (04/2016) | ||
| a) |
Not a rectangle
Sufficient explanation that involves identifying the specific feature of the shape that makes it not a rectangle (i.e., sides not joining/open shape),
Examples of responses
|
very easy |
| b) |
Not a rectangle
Sufficient explanation that involves identifying the specific feature of the shape that makes it not a rectangle (i.e., does not have two sets of parallel lines).
Examples of responses
|
very easy |
| c) |
It is a rectangle
Sufficient explanation involves identifying the specific features of the shape that make it a rectangle (e.g., the shape is closed, has four straight sides, four right angled corners, two parallel lines).
Examples of responses
|
very easy |
| d) |
It is a rectangle
Sufficient explanation involves identifying the specific feature of the shape that makes it a rectangle (e.g., the shape is closed, has four straight sides, four right angled corners, two parallel lines).
Student responses mostly involved saying it was a square not a rectangle. One student noted it was a rectangle but looked like a square. Another student noted: It is a rectangle because it is kind they have all even sides and has four sides.
|
very difficult |
| e) |
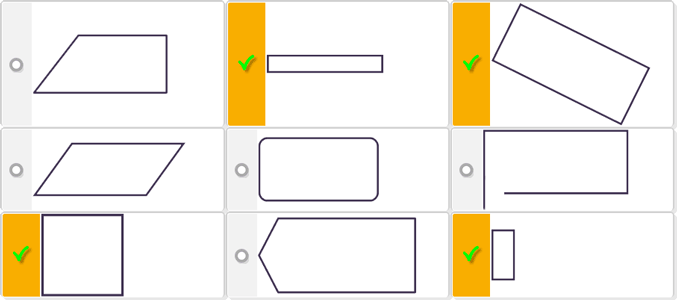 |
All 4 correct - very difficult*
3 correct - moderate
*due to students not identifiying the square as a type of rectangle in d)
|
| f) |
Explanation involves some combination of :
Examples of explanations (with number of identified properties)
NOTE: At this level it might be expected that students provide 1 or 2 properties of rectangles in their explanation for f). A fully suifficient epxlanation could involves 3-4 properties.
|
|
NOTE:
- A shape only needs to lack one property to disprove that it is a rectangle (counter example). However, to show that a shape is a rectangle it should have all properties accounted for - 4 straight sides, 4 right angles/corners, closed, parallel sides, opposite sides are the same length.
- Some dictionaries use the description "especially" to indicate that a rectangle has adjacent sides with unequal length (i.e., 2 short and 2 long sides). For exmaple the online Merriam Webster defines the reactangle as "a four-sided shape that is made up of two pairs of parallel lines and that has four right angles; especially : a shape in which one pair of lines is longer than the other pair". This would support the argument that the square in d) is not a rectangle. However, mathematically, a square is a special type of rectangle, and being aware of this can help students develop a more accurate/sufficient definition of a rectangle.
Teaching and learning:
This resource encourages students to share their understanding about the properties of shapes. In particular, the shape properties that define a rectangle are: a closed plane figure with four straight sides and four right angled corners.
Over-use of a single representation of a rectangle, such as can encourage students to develop a limited sense of what is (and is not) a rectangle. The shapes in this task have been deliberately selected to challenge the "visual protoype" that students may have formed, and to focus attention on the actual geometric properties of rectangles.
can encourage students to develop a limited sense of what is (and is not) a rectangle. The shapes in this task have been deliberately selected to challenge the "visual protoype" that students may have formed, and to focus attention on the actual geometric properties of rectangles.
Over-use of a single representation of a rectangle, such as
In addition, a square has been included to highlight an incomplete understanding of the definition of a rectangle by some students. Including squares when classifying shapes helps to develop students' understanding of the relationships between shapes and their properties, as well as the relationship between "families" of shapes (e.g., a square is a type of rectangle, which is a type of parallelogram, which is a type of quadrilateral, which is a type of polygon, etc).
Diagnostic and formative information:
Insufficient reasons/arguments
Some of the student responses were interesting because of the additional ideas they revealed about their understandings about rectangles and shape properties in general.
Sometimes students may correctly identify whether a shape is or is not a rectangle, but indicate some "developing" concepts, such as
"rectangles have two long and 2 short sides",
"Well, a rectangle is like two squares stuck together without the middle line."
Most students in their explanation tended to use only one property to explain why something is or is not a rectangle. When arguing that a shape was not a rectangle, a single property as a counter example would be sufficient. However, when arguing that a shape was a rectangle, a number of properties needed to be checked. Generally, a single property would be insufficient. For example stating that the shape is a rectangle because it has "four right angled corners" is insufficient, as the explanation doesn't refer to the sides being straight or the shape being closed (both properties of a polygon).
Some of the arguments for a shape not being a rectangle were:
- Because it is uneven/one side is longer than the other side.
- I don't think it is, because all the sides are not the same.
- I think it's not a rectangle because it only has 3 corners.
- Because some of the sides don't touch each other, and one of the sides is also longer than the opposite side.
- Because the corners are not the same.
Arguments that assumed that two sides must be long and two must be short included:
- It has to small sides and to big sides.
- It dose not have two long lines.
- It has four equal sides a rectangle does not.
- 2 lines should be long the other 2 should be a bit shorter.
Some of the arguments for a shape being a rectangle were:
- Because all the lines are straight and connected and it looks exactly like a rectangle.
- It is a rectangle because two sides are the same length and straight, and so is the other side.
- Because its has 4 corner and its like a long square.
- I think it is a rectangle because all the side are straight and even.
Some arguments for being a rectangle did not involve a single property:
- It is a rectangle because I know what a rectangle looks like.
- It is a rectangle turned round.
- Because it is long and straight.
- Because it is the same shape as a re[c]tangle.
- It's a vertical rectangle.
Next steps:
Not correctly identifying a rectangle
Students who identified that questions a) and b) were rectangles and/or that c) and d) were not rectangles, may need to explore the definition of a rectangle. Students could be asked to work in groups to come up with a definition of a rectangle. The images of "rectangles" and "almost rectangles" from this assessment resource could be used to test students conjectures about what defines a rectangle. Some of the student responses included in the Diagnostic and formative information section could also be shared and discussed. Discussion will likely flow to open shapes, and on to what defines a corner and a side. Some of these ideas might need further clarification. Students could be asked to define a corner (and/or side) and develop examples of what a corner (and/or side) is and is not (and why not). Other concepts that might need to be further explored are parallel, right angle, straight lines, even or equal, opposite, etc). Once students have more awareness about sides, corners, and other pproperties they will be more able to determine the important properties for the definition required to define a given shape. Ultimately, it is important to get students noticing and considering the properties of shapes, and using this knowledge to argue whether a shape is or is not a rectangle, or whatever shape - Not relying on remembering the iconic look of a shape (called visual prototype) and using this to compare other shapes.
Incomplete definition
Students who gave brief or incomplete reasons in questions a)-d) and e) could explore the full definition of a rectangle (including the number of sides and right-angled corners). Counter examples could be selectively used for any property that is not accounted for in their definition, e.g., if right-angled corners is not included in the definition, show students a trapezium, or an open "almost rectangle" and then ask them what else might need to be added to the definition of a rectangle to make this complete.
Further sharing of teacher or student definitions that are deemed "sufficient" may also help supplement students' understanding of the range of properties that might need to be included in a definition. A definition for a rectangle could be:
- A four-sided plane figure with four right angles.
- A four-sided shape that is made up of two pairs of parallel lines and that has four right angles
- A polygon with four right-angled corners.
This could be followed by a critique and discussion about sufficiency of the definition.
A square as a type of rectangle
Very few students identified the square as a type of rectangle. This could highlight either students not being aware of a complete definition of a rectangle, or it could be a wider misconception: that students regard shapes as mutually exclusive elements - rather than elements that can be grouped together as families depending upon their properties.
Very few students identified the square as a type of rectangle. This could highlight either students not being aware of a complete definition of a rectangle, or it could be a wider misconception: that students regard shapes as mutually exclusive elements - rather than elements that can be grouped together as families depending upon their properties.
Students with this misconception may need to develop a family tree of the shapes (or quadrilaterals) based upon their definitions to build up their understanding of the relationship between shapes. NOTE: this is referred to as the Van Hiele's "Abstraction" level and needs to build upon student understanding and knowledge of definitions of the shapes they working with.
For further information about shape properties see the Geometric Thinking Concept Map.
For further information about shape properties see the Geometric Thinking Concept Map.

