Angles of a hexagon

Angles of a hexagon

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about interior and exterior angles.
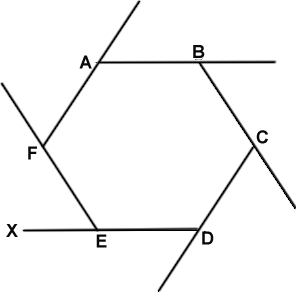
diagram of angles on a hexagon
 
Use the diagram of the regular hexagon above to answer the questions below.
 
a)
Calculate the exterior angle∠FEX. Use the space provided to show your working.
 
 
 
 

∠FEX = __________°
 
b)
Calculate the interior angle ∠ABC. Use the space provided to show your working.
 
 
 
 
 
 
∠ABC = __________°
 
c)
Through what angle would the hexagon have to turn clockwise for point A to get to point E?
 
__________°
Task administration: 
This task can be completed with pencil and paper.
Level:
5
Curriculum info: 
Maths, Geometry and Measurement, Shape
Keywords: 
angles, regular polygons, angle properties, interior angles, exterior angles
Description of task: 
Using a diagram of a regular hexagon, students calculate its interior and exterior angles.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Geometric thinking, set 6
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 

 

Y11 (10/2001)

a)

 60
[NOTE: Full marks given even if working not shown]
Evidence of using one of the following calculations but 1 error made:

  • 360° ÷ 6
  • 180° - 120° (interior angle – see below) = 60°

Interior angle calculation:
180° (n - 2) = 180° × (6 - 2)
                   = 180° × 4
                   = 720°
720° ÷ 6 = 120°

moderate

moderate

b)

 120
[NOTE: Full marks given even if working not shown]
Evidence of using one of the following calculations but 1 error made:

  • 180° - exterior angle
  • 180° - answer given in b)
  • 180° (n - 2) = 180° × (6 - 2)

                        = 180° × 4
                        = 720°
     720° ÷ 6 = 120°

moderate

moderate

c)

240

difficult
Teaching and learning: 
This assessment resource is about the interior angles of a hexagon. Ideally, students will have already explored the relationship between the number of corners (angles) of a shape and  developed a conjecture and then a generalised rule about the relationship between the number of sides of a shape (polygon) and the sum of interior angles. For example, they could explore a range different (regular and irregular) variations of common polygons, and measure and sum the interior angles (noting the relationship with the exterior angles), and then look at the pattern to develop a conjecture, followed by a generalised rule about sum of interior angles = number of sides x  180°.
 
Shape Sides Sum of interior angles
Triangle 3 180°
Quadrilateral 4 360°
Pentagon 5 540°
Hexagon 6 720°
Octagon 8 1080°
 
Diagnostic and formative information: 
  

Common errors

Likely miscalculations

Likely reasons

a)


b)

120


60

360° ÷ 6 = 60°
180° - 60° = 120°
or (4 × 180°) ÷ 6
360° ÷ 6
or 180° - 120°

Confuses interior and exterior angles.

 

 

c)

180

60° × 3

Only rotates hexagon 3 times.