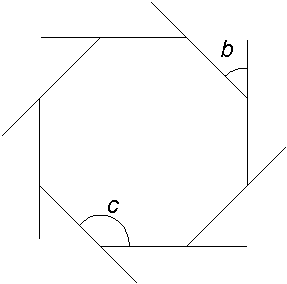
Angles of an octagon

Angles of an octagon

Pencil and paperOnline interactive
Overview
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about angle properties.
octagon-lines.png
The shape above is a regular octagon.

Question 2Change answer

a)  The centre of Dunedin is called the Octagon. If you walked right around the Octagon once,
    how many degrees would you have turned through?  º

Question 2Change answer

b)  i)  What is the size of angle b?  º
ii) How did you work it out?

Question 2Change answer

c)  i)  What is the size of angle c?  º
ii) How did you work it out?
Level:
5
Curriculum info: 
Maths, Geometry and Measurement, Shape
Keywords: 
angles, regular polygons, angle properties, interior angles, exterior angles
Description of task: 
Students calculate the interior and exterior angles of a regular octagon and explain their calculations.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Geometric thinking, set 6
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 

 

Y11 (05/2000)

a)

 

360

moderate

b)

i)
ii)

45 [Accept answer to a) ÷ 8].
Any 1 of:

•   360º ÷ 8 [Accept answer to a) ÷ 8].
•   Exterior angles sum to 360º.
•   180º - 135º or angles on a straight line if
     c)i) and c)ii) both correct.

easy
moderate

c)

i)
ii)

135 [Accept 180 - answer to b) i)].
Any 1 of:

•   180º - 45º.
•   [Accept 180º - answer to b) i)].
•   Angles on a straight line (sum to 180º).
•   Sum of interior angles = 1080º.
•   180º (n - 2) = 180º × 6 = 1080º.
•   1080º ÷ 8 = 135º.
•   Number of internal triangles × 180º ÷ 6.
•   90º + 45º if b)i) and b)ii) both correct.
•   Other equivalent explanations.

easy
moderate
Teaching and learning: 
This assessment resource is about the interior angles of a octagon. Ideally, students will have already explored the relationship between the number of corners (angles) of a shape and  developed a conjecture and then a generalised rule about the relationship between the number of sides of a shape (polygon) and the sum of interior angles. For example, they could explore a range different (regular and irregular) variations of common polygons, and measure and sum the interior angles (noting the relationship with the exterior angles), and then look at the pattern to develop a conjecture, followed by a generalised rule about sum of interior angles = number of sides x  180°.
 
Shape Sides Sum of interior angles
Triangle 3 180°
Quadrilateral 4 360°
Pentagon 5 540°
Hexagon 6 720°
Octagon 8 1080°
 
Diagnostic and formative information: 

 

 Common error

Likely calculation

Likely reason

a)

1080

(8 - 2) × 180

Confuses interior and exterior angle.