Commutative number lines II
This task is about using number lines to show number sentences.
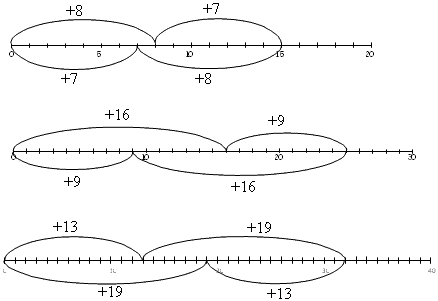
a) Write the number sentence that each number line shows in the boxes below.
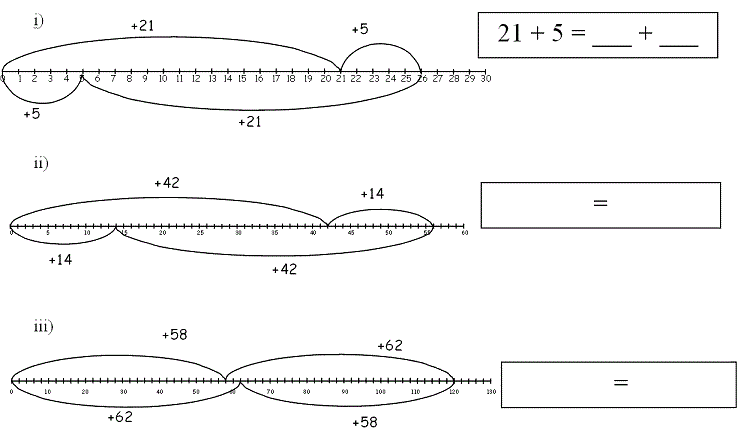
|
b)
|
Use the number lines below to draw in each number sentence.
|


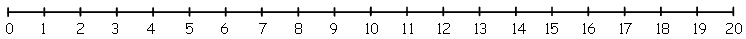
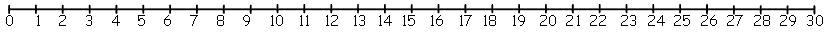
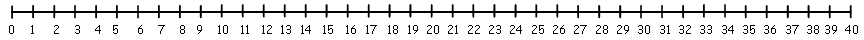
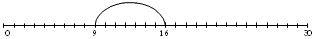
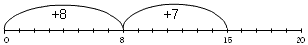
 + 29 = 81.
+ 29 = 81.