Corners and sides II
0
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about shapes.
Shapes have corners and sides.
Task administration:
This task can be completed with pencil and paper or online (with auto marking displayed to students).
Copyright:
Image copyright: NZCER
Levels:
1, 2
Curriculum info:
Keywords:
Description of task:
Students identify shapes with given shape properties.
Curriculum Links:
This resource can help to identify students' understanding of the properties of shapes.
Conceptual maps:
For further information about geometric thinking, refer to the Geometric Thinking Concept Map, in particular Properties and Classification of Shapes.
Learning Progression Frameworks
This resource can provide evidence of learning associated with within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.Answers/responses:
| Y3 (04/2016) | ||
| a) |
 |
All 3 correct - very difficult
At least 2 correct - very difficult
At least 1 correct - moderate
|
| b) |
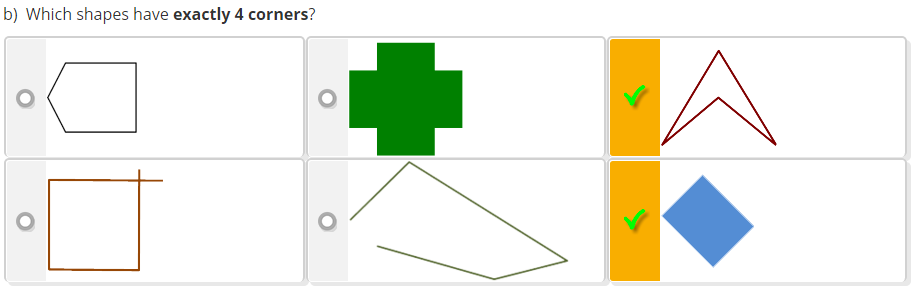 |
2 correct - very difficult
At least 1 correct - moderate
|
| c) |
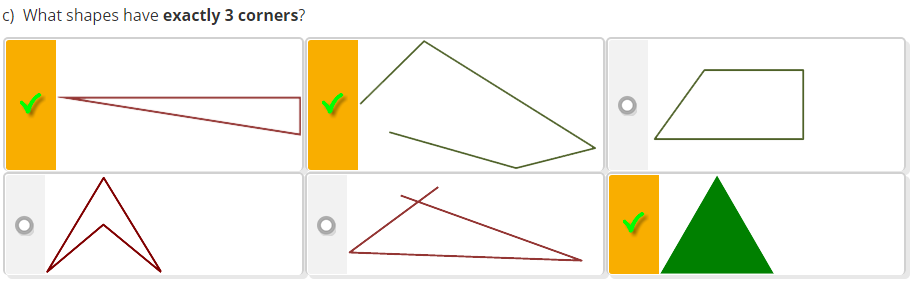 |
All 3 correct - very difficult
At least 2 correct - very difficult
At least 1 correct - moderate
|
| d) |
 |
All 3 correct - very difficult
At least 2 correct - difficult
At least 1 correct - easy
|
Based on an online sample of 47 Y3 students.
Teaching and learning:
This resource is about getting students to classify 2-D shapes based on their attributes or properties, rather than by their name or what they look like. Students are encouraged to identify the properties of sides and corners rather than shape names such as 'square', 'triangle' or 'rectangle'. It is anticipated that there will be some disagreement amongst students which can lead to rich discussions about the nature of shape classification.
Diagnostic and formative information:
Students found it easiest to recognise the properties of simple, closed polygons with no concave angles such as  ,
, ,
,  ,
,  ,
,  and
and 
 ,
, ,
,  ,
,
These shapes can be considered to be icons (or visual prototypes) of familiar shapes such as rectangles, triangles or pentagons (as outlined in the Properties and Classification of shapes section of the Geometric Thinking Concept Map).
Students therefore recognise these shapes from their overall appearance rather than from observation of their properties.
| Common error | Likely Misconception |
|
Not all sides of the polygon are counted:
 Students may only count the visually dominant sides of the shape and not include the sides in between. Students may only count the visually dominant sides of the shape and not include the sides in between. Students may see this as a triangle, therefore assume it has three, rather than four, sides. Students may see this as a triangle, therefore assume it has three, rather than four, sides. |
Students rely on visual prototypes of shapes. |
|
Not all corners of the polygon are counted:

Students may not count the internal/concave corner or they may see this as a triangle which therefore only has three corners.

Students may count four sides and assume there are also four corners or they may see 5 corners.
 
Students may not have encountered polygons that have overlapping sides and may not have counted the three additional corners created by the overlapping lines.
|
Students do not have a clear understanding of what defines a corner. |
Next steps:
Students rely on visual prototypes of shapes.
Expose students to a wide range of regular and irregular shapes that do not resemble the visual icons or prototypes of triangles, squares, rectangles or pentagons.
Expose students to a wide range of regular and irregular shapes that do not resemble the visual icons or prototypes of triangles, squares, rectangles or pentagons.
Teachers and/or students could draw large shapes on the playground or use tape to create them in the classroom.
Students could then walk around the shapes or stand on each side of the polygon and discuss how many sides there are in that particular shape. This could lead to a discussion about what defines a side.
Individual students, pairs, groups or the whole class can go on "Shape Walks" and find different shapes, identifying their properties rather than naming them. Photographs for sharing, further discussion or display could be taken.
Students do not have a clear understanding of what defines a corner.
While students have often rememebered that a square or rectangle has four corners and a triangle has three, when they meet shapes with overlapping lines, or open shapes, they may find it difficult to work out how many corners the shape has without a definition of what a corner is.
This can lead to rich classroom or group discussions about the definition of a corner. Students can work together to define what a corner is and then count the corners on open shapes or shapes with extending/overlapping lines.
Teachers or students drawing large shapes in the playground or using tape to create them in the classroom can assist with these discussions.
Mathematically, a corner is described as being "a place or angle where two sides or edges meet". Teachers could draw a large '+' on the board and ask "How many corners does this shape have?" to initiate discussion and debate.
To help students focus on the properties or features of a shape, have them describe a given shape without using the name of the shape. This could be done as a barrier game where students have the same set of shapes in front of them, with a barrier between them. The first student describes a shape to their partner, without reference to its name, and the partner has to identify the shape from their own set.

