Health percentages

Health percentages

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about writing percentages as decimal numbers.

Six friends are playing a computer game called CONQUEST. The health of their characters is shown on the screen as percentages.

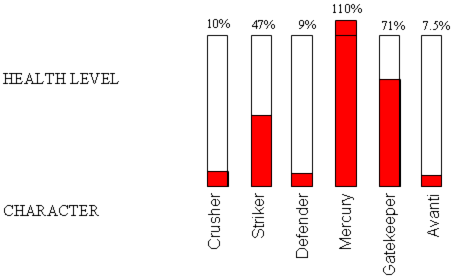
Write each character's health percentage as a decimal in the table below.

Character Percentage Decimal
Crusher 10% a)
Striker 47% b)
Defender 9% c)
Mercury 110% d)
Gatekeeper 71% e)
Avanti 7.5% f)

 

Task administration: 
This task is completed with pencil and paper only.
Level:
4
Curriculum info: 
Maths, Number and Algebra, Number Knowledge
Keywords: 
decimals, decimal fractions, percentages
Description of task: 
Students convert percentages to decimal numbers.
Answers/responses: 
    Y8 (05/08)
a) 0.1  [also accept .1, 0.10, .10 or other correct decimals] easy
b) 0.47  [also accept .47 or other correct decimals] easy
c) 0.09 [also accept .09 or other correct decimals] moderate
d) 1.1 [also accept 1.10 or other correct decimals] easy
e) 0.71 [also accept .71 or other correct decimals] easy
f) 0.075 [also accept .075 or other correct decimals] difficult

Based on a representative sample of 228 students.

Diagnostic and formative information: 
  Common errors Likely misconception
a)
b)
c)
d)
e)
f)		 10
47
9
110
71
7.5		 Students do not know how to convert from percentages to decimals. They try:
1.  simply dropping the percentage sign;
2.  adding a decimal point (e.g., 10., 47., etc.); or
3.  adding a decimal point with a number of zeros following (e.g., 10.0, 10.00, 47.0, etc.).
a)
b)
c)
d)
e)
f)		 1.0
4.7
0.9
11
7.1
0.75		 Students are aware that converting from percentages to decimals can involve moving a decimal point (varying place value) however they move only one place in the correct direction. 
This was a very common strategy used. Especially in c), the student may not understand the role of zero as place holder in decimals.
a)
e)		 0.01, 0.010, .1 etc.
0.11, 0.110, .110		 Students are aware that converting from percentages to decimals can involve moving a decimal point (varying place value); however they move only one place and in an incorrect direction.
f) 0.07.5, 0.07 ½ , etc. Students are unsure what to do with decimal percentages, so devises their own notation for it (including using more than one decimal point).

Alternative correct responses
Students who give the alternative answers given in parentheses in the answers/responses, are generally less mathematically competent than those who give the first answer that is given. These students may still have a limited understanding about constructing decimals from percentages. For example they may simply move the decimal point along to the left without understanding why.

Next steps: 
Using a range of incorrect strategies
Students used one of a number of different strategies such as:

  1. simply dropping the percentage sign;
  2. adding a decimal point; or
  3. adding a decimal point with a number of zeros following.

Students may need to look at the meaning of the percentage: a percentage is equivalent to a fraction with a denominator of 100, so 47% = 47/100.
For ARB resources that are related to the meaning of percentages click on the keywords or on the link, percentages AND place value.

Knowing to moving the decimal point
Students who know to move the decimal point two places to the left to convert percentages to decimals need to explore in more depth the place value meaning of decimals.  For example:

  • 1 can be got by cutting up 10 into 10 equal parts, each of which is called 0.1;
  • 0.1 can be got by cutting 1 up into 10 equal parts, each of which is called 0.01;
  • 0.01 can be got by cutting 0.1 up into 10 equal parts, each of which is called 0.001; etc.

Not able to convert one-digit numbers
Some students can convert percentages of two digit numbers to decimals, but not one-digit numbers.  These students may have learnt a simple strategy that works for many problems, but not all.  In particular, they may still not fully grasp the significance of zeros place holding digits in decimals. For example, they may not see that 0.9 is different from 0.09. Use the analogy from whole numbers that 1, 10, and 100 all have different meanings, just like 0.1, 0.01, and 0.001, etc.

Cannot convert percentages with a decimal part
For students who cannot convert percentages that have a decimal value in them, explore the role of thousandths, i.e.:

  • 0.001 can be got by cutting 0.01 up into 10 equal parts; then
  • 10% = 0.1, so 1% is 0.1 cut up into 10 pieces = 0.01;
  • 1% = 0.01, so 0.1% is 0.1 cut up into 10 pieces = 0.001;

So Place value partitioning of 0.275 into 0.2 + .07 + .005 is equivalent to
20% + 7% + 0.5% = 27.5%.

Class discussion
A class discussion about how they solve the problem "does it work for all decimals?”, and “What ways are there of writing percentage such as 0.5%". 

See Mathematical classroom discourse for more information on this assessment strategy.