Making more stick patterns
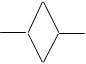
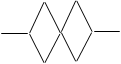
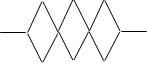
| Shape | Number of sticks |
| 1 | 6 |
| 2 | 10 |
| 3 | |
| ... | ... |
| 7 | |
| 10 | |
| 15 |
For example, write a rule that would help work out how many sticks are neeed to make Shape 100.
| 1) | Students make the first 3 shapes. |
| 2) |
Students construct and draw shape 6.
|
| 3) | 14, ..., 30, 42, 62 |
| 4) |
Students describe the number of sticks needed for given shape numbers, e.g., Sequential relationship (+4)
Direct or functional relationship (4n + 2 or 6 + 4(n – 1))
|
These questions have been phrased to encourage a functional (direct) rule which can be applied to find an nth term of a pattern, rather than a sequential rule which relies upon the previous term/s. The use of a sequential rule can be compared to using an additive strategy (repeated addition). The use of a direct/functional rule can be compared to using a multiplicative strategy. This spatial pattern quite clearly shows the two components (initial term and difference, see Arithmetic progression (Wikipedia).
Prior knowledge
This resource explores describing patterns with a rule. One important part of this that students need to be aware of is that the rule should apply to all elements in the pattern – not only the first or the most recent member.
All students in the pilot of this resource could make the shapes in a) and b). The table in question b) is set up to encourage students to look at the relationship across the rows (direct) rather than down the Number of sticks column (sequential). A number of students correctly described a sequential rule (add three each time). Some students identified a direct rule. This can develop from the recognition that for every iteration there are 4 more sticks added and connecting this "so you multiply by 4" (and "don't forget the start: 2 sticks either side of the pattern").
| Common error | Likely misconception | |
| 3) | 14, 18, 22, 26 |
Not looking at the shape number and only continuing a sequence of +4 Students only use the +4 and don't notice that the shape numbers are not in order. |
| 3) | 15, 35, 50, 60 |
Students who described an incorrect/insufficient rule Although they are working across the table students have ignored the intercept and used an incorrect rule: using the last shown row shape number 2 = 10 sticks (× 5). |
Not able to identify the number of sticks for the next shape
Students who could not identify the number of sticks needed to make "the next shape" could be asked to identify the number of sticks in earlier shapes (1, 2, and 3) and then asked how many more sticks might be needed for the next shape. Students could also be given an opportunity to construct growing patterns and explore the increase and the starting point [see resources: Making stick patterns, Making triangle patterns and Building square patterns].
Cannot adequately write a rule for the pattern
For students who could not write a rule to describe the growing pattern get them to explore situations where they continue or construct patterns (see above). Once they can continue a pattern encourage them to orally describe what is happening to the pattern and to identify the parts that are increasing and what stays constant. The resources Match patterns, and Continue the shape patterns look at developing sequential rules for growing spatial patterns at Level 2. Students could share their rules for the patterns in small groups and check that each others' rules work for allshapes of the pattern (see Providing a sufficient explanation-Peer assessment below). Once students can identify the sequential rule they could look at developing a functional rule (see Students who described a sequential rule below). Continue the shape patterns also provides the opportunity to describe a functional (direct) rule.
Not taking into account the single stick at the start of the pattern
Get students to create more shapes of each pattern. Ask, "Does Shape 6 have twice as many sticks as Shape 3?" or "Does Shape 3 have three times as many as Shape 1?" For question a) remove the two horizontal sticks from all the shapes and ask how the pattern grows. Compare this to the original pattern and ask what the difference is, and how this changes the rule. The two horizontal sticks are the intercept (2). This should help students see how the intercept influences the pattern.
For example in question a) the first shape has 2 + 4 sticks, the second 2 + 4 + 4, etc, so the 2 is the initial term of an arithmetic progression (as well as the intercept) and the 4 is the common difference (or increase) – which becomes the number that n is multiplied by in the functional rule for the pattern.
Students who described a sequential rule
For students who described a sequential rule, ask them how they might find a rule that would work for any given number, e.g., How many sticks for shape 100? Trying to use the sequential rule should be unwieldy and the need for a functional rule can become evident. It can also mean that students do not develop an understanding about patterns with an intercept. Additionally, as students apply their sequential rule they may see the connection between the number of sticks they add on to the previous shape and the number that n (shape number) is multiplied by in the functional rule.
Students who described a functional rule with some errors
For students who described a functional rule, but made some errors, encourage them to share and explain their rule, and check that the rule works for all members of the pattern – not just the first two. Using shape numbers like 10 and 100 make it easier to see the relationship in the pattern, e.g., 4n + 2, for n = 100 is 402. Encourage students to include examples to help clarify their description of the pattern. A small group discussion should provide peer support to re-check the completeness and accuracy of their rule.
Students giving "just sufficient" explanations – Peer assessment
Many of the students gave explanations that were "just sufficient", but did not fully describe or explain how they worked it out. These students could share their explanation (or explanations from this resource) in a group to identify details and clarify ideas that are needed in their explanations. Students could develop criteria for an explanation and do some peer assessments. They could also have a "sufficient" explanation modelled and made explicit to them (by other classmates or the teacher). A criteria* of what makes an explanation sufficient might be:
- specific details;
- appropriate use of or reference to examples;
- justification;
- clarity to another reader.
*Get the students to develop the criteria they will use.
Click on the link to the English resource (Writing an explanation) for further information or ideas about supporting self-assessment of writing explanations.


