Number line addition II

Number line addition II

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing how to solve addition equations on a number line.

For the questions below show how to solve the equations on the number line. Read the example below before you start.

Example: For the equation: 46 + = 70,
Sarah used tidy numbers to show the answer on a number line. She knew that 46 + 4 = 50, and then 50 + 20 = 70.

So she showed this on the number line and        wrote the answer in the box:
 
 
a)
 
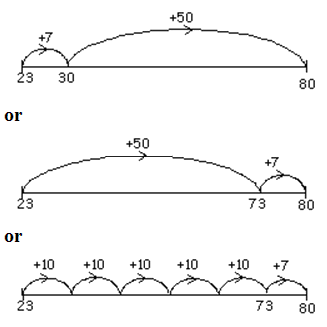
Show how to solve the equation: 23 +  = 80 on the number line below
 
 
 
 

 
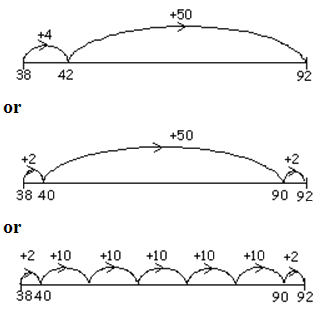
b) Show how to solve the equation: 38 +  = 92 on the number line below.
 
 
 
 

 
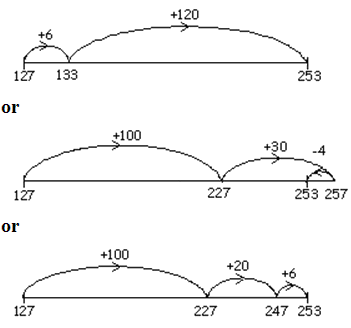
c) Show how to solve the equation: 127 +  = 253 on the number line below.
 

 
 
Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
number lines, addition
Description of task: 
Students use a number line to show how to solve whole number addition problems.
Curriculum Links: 

This resource can help to identify students' ability to use basic addition facts and knowledge of place value to partition whole numbers.

Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
   

Y7 (03/2005)

a)

57
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

easy
moderate

b)

54
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.

moderate
moderate
c) 126
The number line is used to show jumps added/subtracted that use the sequential nature of the number line, e.g.,

or other acceptable jumps that show the equation.		 moderate
moderate
Results based on a sample of 220 students.
 
NOTE:

  1. Accept even if arrows are missing, as long as the intent is clear.
  2. This assessment is about showing how to solve a problem using a number line (communicating mathematical ideas). The number line examples given in the answers to questions a)-c) are ordered approximately from the most efficient to least efficient use of jumps.
Teaching and learning: 
This assessment resource is about whether students can show the process of solving an addition equation on a number line and what strategies they use to do so, rather than whether they can solve an addition equation. Students who have not used a number line to solve problems will need to learn how to show addition and subtraction jumps on a number line.
Next steps: 
The place value partitioning shown in the last examples for questions a) and b) indicates an early additive part-whole as the jumps are unitized, not grouped (i.e., 10 + 10 + 10 + 10 instead of + 40). To indicate advanced additive thinking, students would use fewer numbers of jumps (more efficient jumps) to solve equations and be able to use or identify different ways to show how to solve the equation (multiple strategies).

Figure it out: Maths Detective (Number sense and Algebraic thinking, L3, book 2, pages 2-4), and Tidying up (Number sense and Algebraic thinking, L3, book 1, pages 2-4).

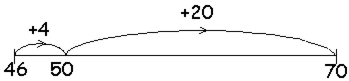
Numeracy: Using tidy numbers: refer to Jumping the number line, Problems like 23 +  = 71, and for using place-value partitioning: refer to Problems like 37 +  = 79 (both Book 5: Teaching addition, subtraction and place value, pages 33-36).
 
Links to the Numeracy project

Showing how to solve addition problems on a number line can require jumping to tidy numbers, or using tidy numbers to make the jumps, and then making an adjustment to complete the equation. Students can also use elements from place value partitioning, or compatible numbers, to jump along the number line.