Number line addition and subtraction III

Number line addition and subtraction III

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing how to solve addition & subtraction problems using a number line.
For the questions below show how to solve the equations on the number line. 
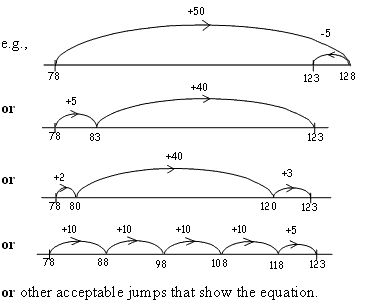
a) Use the number line below to show how to solve the equation: 78 +  = 123
 
 
 
 
 
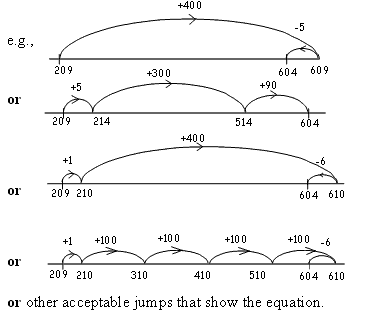
b) Use the number line below to show how to solve the equation: 209 +  = 604
 
 
 
 
 
c) Use the number line below to show how to solve the equation: 230 -  = 125
 
 
 
 
 
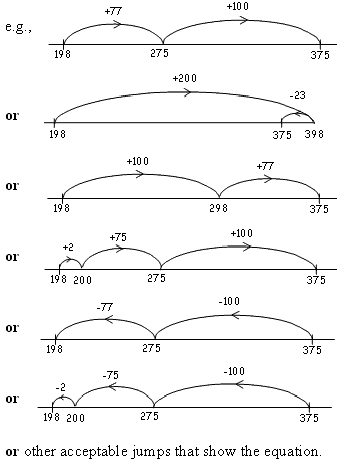
d) Use the number line below to show how to solve the equation: 375 -  = 198
 
 
 
 
 
Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
number lines, addition, subtraction
Description of task: 
Students use number lines to show how to solve whole number addition and subtraction problems.
Curriculum Links: 
This resource can help to identify students' ability to apply additive and simple multiplicative ideas flexibly to combine or partition whole numbers to solve addition and subtraction problems.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Additive thinking, sets 6-7
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
    Y7 (03/2005)
a) 45
The number line is used to show jumps added/subtracted that use the sequential nature of the number line,
 easy
moderate
b) 395
The number line is used to show jumps added/subtracted that use the sequential nature of the number line,
 easy
moderate
c) 105
The number line is used to show jumps added/subtracted that use the sequential nature of the number line,
 easy
easy
d) 177
The number line is used to show jumps added/subtracted that use the sequential nature of the number line,
 easy
moderate
NOTES:
  • Accept even if arrows are missing, as long as the intent is clear.
  • The number line examples given in the answers to questions a)-d) are ordered approximately from the most efficient to least efficient use of jumps.
Teaching and learning: 

This assessment resource is about whether students can show the process of solving an addition/subtraction problem on a number line and what strategy/ies they use.

Diagnostic and formative information: 
  Common error Likely misconception
c) 115 Addition/subtraction error:
230 – 125 = 115, i.e., 25 +15 = 30.
b)
d)		 405
223		 Some partitioning but swapping the direction of the subtraction operation to subtract the smaller number, e.g., for 375 - _____ = 198
→ 300 - 100 = 200 and 98 - 75 (swapped around) = 23

Approximately one third of students solved the subtraction by setting up the problem as an addition problem and adding the jumps (called complementary addition).  These students had a slightly higher success rate (getting the right answer), most likely due to fewer errors being made using a simpler operation (addition).

Next steps: 

For students who could not use the number line to show any of the problems, they may need to work with other materials (abacus, tens frames, or representations) to develop the understanding that numbers can be decomposed and recomposed.

For all students, sharing their own strategies and critiquing them to find more efficient or easier ways to perform the problems is a next step. Getting students to then apply a range of strategies to solve different problems is a good way to develop a better understanding of both the addition and subtraction strategies.

Links to the Numeracy project
The place value partitioning shown in the last examples for questions a) and b) indicates an early additive part whole thinking as the jumps are unitised based on place value, not grouped (i.e., 10 + 10 + 10 + 10 instead of + 40). 
To indicate advanced additive thinking, students would use fewer jumps to solve equations and be able to use or identify different ways to show how to solve the equation (multiple strategies) and to critique these strategies.  Extension: This resource could be adapted to require students to show a range of strategies that could be used to solve one of the equations.

Figure it out:
  • Maths Detective (Number sense and Algebraic thinking, L3, book 2, pages 2-4), and
  • Tidying up (Number sense and Algebraic thinking, L3, book 1, pages 2-4).
 
Numeracy
Using tidy numbers: refer to Jumping the number line, Problems like 23 + ?  = 71, and for using place-value partitioning: refer to Problems like 37 + ?  = 79  (both Book 5: Teaching addition, subtraction and place value, pages 33-36).