Show the fraction

Show the fraction

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing a fraction on a number line.
 
a)
Put a cross on the number line to show where \(3 \over 7\) would be.
 
 

 
b)
 
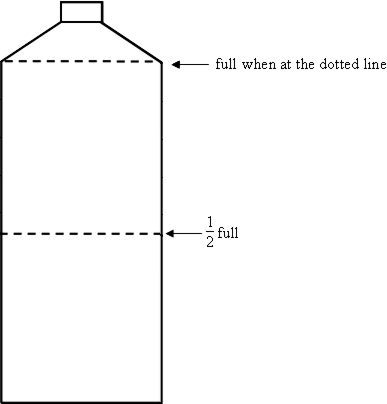
Put a mark on the milk bottle to show where the milk would come to if it was \(5 \over 9\) full.
 

 

Task administration: 
This task is completed with pencil and paper only.
Levels:
3, 4
Curriculum info: 
Maths, Number and Algebra, Number Knowledge
Keywords: 
fractions, number lines, fractions as measures
Description of task: 
Students show fractions on a number line and on the side of a milk bottle.
Answers/responses: 
    Y6 (11/2005)
a) Student responses were coded into regions on the number line as follows:

  • Region A – acceptable degree of accuracy
  • Region B – less accuracy  [insufficient accuracy]
  • Region C – correct side of a half  [insufficient accuracy]
  • Region D – incorrect side of a half  [incorrect].

NOTE: On the students' page the number line is 14 cm long to make it easier to measure the partitions accurately.

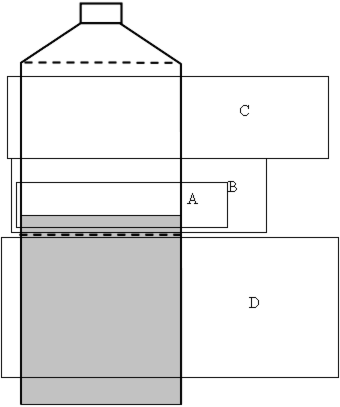
 difficult
(Region A)
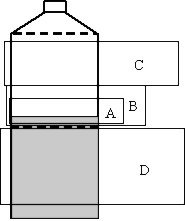
b) Student responses were coded into regions on the milk bottle as follows:

  • Region A – acceptable degree of accuracy
  • Region B – less accuracy  [insufficient accuracy]
  • Region C – correct side of a half  [insufficient accuracy]
  • Region D – incorrect side of a half  [incorrect].

NOTE: On the students' page the milk bottle is 9 cm high to make it easier to measure the partitions accurately.

 difficult
(Region A)

Based on a representative sample of 173 Y6 students in November 2005.

NOTES:

  • There is a marking template at the end of this resource.
  • The most accurate answers for a) and b) were achieved by students who showed some evidence of how they partitioned the number line (or the milk bottle) into equal parts before marking their answer.
Teaching and learning: 
  • Using a milk bottle is similar to using a number line in that they both deal with length (1-Dimension).
  • Milk bottles were chosen because most students will be familiar with fractional discussion about the how full the bottle is, e.g., "the bottle is half empty", "there's about a quarter of a bottle left" etc.
  • The apparent 2-dimensional nature of the milk bottle tends to make it easier for students to visualise and break it down into parts (partition).
Diagnostic and formative information: 
Likely misconception Example
Lack of understanding about representing fractions
Students may know that 3/7 is somewhere less than a half (or 5/9)  is somewhere more than a half), but they don't have a way (strategy) of identifying how far along the number line the fraction is.		 Puts a mark in region C for either question a) or b)
Not recognising a fraction as a number
(applying rules for natural numbers)
This may indicate that students don't recognise a fraction as a single number, but as two numbers, and apply the rules for natural numbers (counting numbers), e.g.,
" 3/7 is somewhere more than a half because 3 and 7 are greater than 1 and 2" and
" 5/9 is greater thanbecause 5 and 9 are greater than 1 and 2".		 a) Puts a cross in the region D
b) Draws a mark across region C
This could indicate that students:

  • did not know what the "whole" was, and were trying to find a fraction of some other "part", e.g., findingof "half" the milk bottle; or
  • Students did not understand what parts of a fraction actually represent.
 b) Draws a mark across region D

 

Next steps: 
Students may "guess" where the milk level is, so it is important to encourage students to:

  • explain how they worked it out;
  • explain how they know their method works (critique their answer and strategy);
  • show this using diagrams, mathematical notation or writing explanations.

Getting students to talk about their strategies and thinking provides information for formative feedback. Students whose response lay in region B (for both questions) should be encouraged to show how they could check the accuracy of their answer.  It may be an issue of needing more care when partitioning evenly. Students who marked the fraction on the correct side of a half [response: region C for a) & b)] may need to clarify what the "whole" is before they start to find the fraction:

  1. Ask them to describe how they know that is where the mark is supposed to be, and how they could check that this is correct.
  2. Encourage them to show how they constructed the answer, e.g., partitioning the entire number line (or milk bottle) into equal parts and then adding each unit fraction to make the fraction shown.
  3. If students are having difficulty, use questions like
    "How far along the number line (or bottle) would half way be?"
    "… a quarter of the way be?",
    "How far along (or up the bottle) is(or)?", and then count up to (or).

Students who indicated the fraction on the incorrect side of a half may also need more experiences partitioning shapes and number lines into pieces and relating the number of pieces to the bottom number, and building up non-unit fractions (and naming them) using these pieces.  Then try steps 1-3 above.

Marking template
Photocopy onto acetate and use to mark students work.