Ordering bottles

Ordering bottles

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about showing what fraction of a bottle is filled.
\(1 \over 2\) \(3 \over 4\) \(1 \over 3\) \(1 \over 4\) \(1 \over 5\) \(2 \over 3\)

 

Choose the correct fraction to show how full each bottle is. 

Write the fraction underneath the bottle. 

 

          ________          ________           ________          ________          ________          ________

Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Knowledge
Keywords: 
fractions, fractions as measures, ordering fractions
Description of task: 
Students match given fractions to images of milk bottles to show how full each bottle is.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
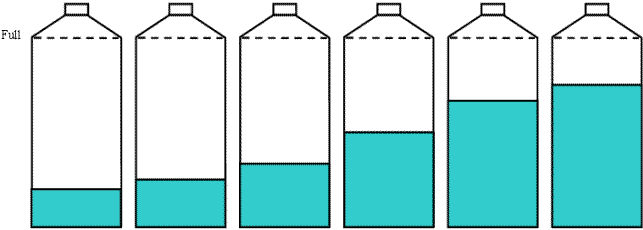
    Y4 (11/2006)
1/5 , 1/4 , 1/3 , 1/2 , 2/3 , 3/4 [an error could be a transposition, swapping, or scribing error]
For all 6 correct
For 1 error
difficult
difficult

Based on a representative sample of 183 students.

Teaching and learning: 
This resource uses representations to support student visualisation of fractions.  It is intended to support their understanding that fractions have a size and can be compared.  Milk bottles and their fullness is a common context for many children.  It may help them make connections between fractions and their informal language of proportion.
Diagnostic and formative information: 
HalfAlmost two-thirds of students correctly labelled the fourth bottle as 1/2 . This may indicate their prior knowledge about the size of a half.  Conversely, almost a quarter placed the 1/2 as the first fraction indicating their lack of understanding about a half (the most common fraction).

Three quartersOver half of the students placed 3/4 in the correct place (the last bottle).  This could be because they were aware that 3/4 is greater than 2/3 .  However, students could have selected the right answer for the wrong reason: 3 is the largest numerator so it must be the largest, or 3 and 4 can be added or multiplied to be larger than any other numbers.  It is important to ask students to explain why they know where the fraction goes and how they know that one is larger or smaller than adjacent fractions.  The reasoning and strategies used can provide valuable insight into their fractional understanding.

One fifthOver a third of students correctly labelled 1/5 .  This is likely to indicate they understand that 1/5 is the smallest fraction, and have some exposure to rules for unit fractions like the bigger the number on the bottom the smaller the fraction – this is still not a sufficient indication of really understanding why 1/5 is the smallest and students should be asked to explain their reasoning.

NOTE: Students may also be having difficulty with the fraction notation and it may be prudent to be aware that their prior experience may involve the name but not the notation.  For example they may know how much three-quarters is, but not that 3/4 is three-quarters.

Common error Likely misconception
1/2 , 1/3 , 1/4 , 1/5 , 2/3 , 3/4 Whole number misconceptionAbout 10% of the sample gave this answer.  It can show a misconception about the relationship between the denominator and numerator.  Students believe that the smaller the numbers in the fraction the smaller the fraction.  This "rule" works for whole numbers, but does not apply to all rational numbers.Students may try to relate the two numbers by ordering the numerators and then the denominators either in descending or ascending order.
1/2 , 3/4 , 1/3 , 1/4 , 1/5 , 2/3 This is the same misconception as above but students have made a transposition error, putting the 3/4 after the 1/2 .
1/3 , 1/4 , 1/5 , 1/2 , 2/3 , 3/4 This is similar to the above misconception except that students have placed the half correctly, possibly indicating their application of prior knowledge about the size of half. About 4% of the sample answered with this misconception.
Next steps: 
Students who have the whole number misconception identified above need to develop a part-whole understanding of fractions before trying to devise a system to order or compare fractions.  A part-whole understanding of fractions is about recognising that a fraction is a part of a whole, and that it is the relationship between the top and bottom number that describes and quantifies the fraction, i.e.,  it is about the relationship between the numbers, not their absolute size.  Students should be aware that the bottom number represents how many parts make up the whole, and the top number represents how many of these parts are of interest.

If required, students could go back to partitioning and explore constructing the parts (unit fractions), combining these parts to make non-unit fractions, and naming these new fractions.  Encourage students to explore a range of many new fractions such as 1/8 , 3/7 , etc.  After this, encourage students to compare just two fractions (including non-unit fractions) before trying to order a number of unit and non-unit fractions.  Appropriate drawing of fractions can promote understanding and help with comparing the size of fractions.

For students who misplace one fraction such as 2/3 , 3/4 , or 1/5 , ask them to explain how they know that the misplaced fraction is larger or smaller than adjacent fractions.  For a resource comparing fractions see Larger fractions. For students who could place all six fractions correctly, ask them where they think 2/5 , 3/5 , 4/5 , or 3/2 may fit in the order.  Ask students to explain their reasoning.

 

For more information on fractional thinking, click on the Fractional thinking concept map.