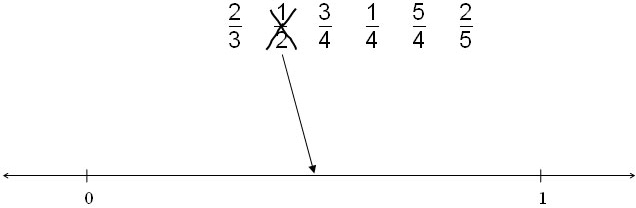
Fractions on a number line
For each of the fractions below draw an arrow to where it fits on the number line.
12 has been done for you.
| Y6 (11/07) | |
|
1/4 2/5 2/3 3/4 5/4 |
easy moderate moderate easy moderate |
|
Accurately (within the orange box) mark 5 fractions 4 fractions 3 fractions NOTE: A certain margin of error was applied to the positions on the number line and this was used to work out the difficulty levels. Below is an approximate marking guide for accuracy. The red circle indicates "very accurate" marking, and the orange box indicates "accurate" marking which was used to construct the difficulty levels.
|
difficult difficult moderate |
Number lines can also support the understanding fractions as rational numbers, and be used illustrate the idea of density.
Just over 10% of students marked all five fractions very accurately. The results, accepted accuracy, and difficulty level for each fraction are shown in the table below
| Fraction | High accuracy red circle | Less accuracy orange box* | Difficulty level Accepted accuracy |
|
1/4 2/5 2/3 3/4 5/4 |
54% 34% 37% 46% 34% |
10% 7% 13% 18% 7% |
easy (64%) moderate (41%) moderate (50%) easy (64%) moderate (41%) |
* excluding red circle
The fraction that students placed farthest from its actual location value was 2/5 . Almost a third of students placed 2/5 between 3/4 and 1 on the number line. Over a third of students also marked 5/4 in that quadrant (being close to the actual location near to one, but below instead of above one). Students with a whole number misconception about fractions are likely to mark 5/4 here as it is the largest fraction because the numbers are the largest (either treating the numbers separately or combining them in some way – often by adding). Another misconception that contributes to this placement of 5/4 is a belief that all fractions are under 1. Even the meaning of the word fraction as "a part of" supports this misconception.
A surprising number of students marked 1/4 in the quadrant before 1. With 1/2 marked, 1/4 should really have been the easiest fraction to mark accurately (as almost two-thirds did). Nevertheless almost a sixth of students marked it quite far away, which indicates some misunderstanding about fraction size on a number line (or even use of a number line to represent fractions). To support students who have this misunderstanding point out the 1/2 and explain it is half way between 0 and 1, and then ask where they think a 1/4 would go. The resource Walking to school explores connecting the language of distance with positions on a number line.
Marking template
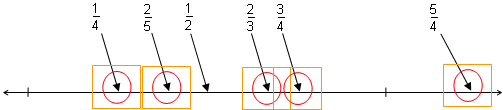
Very inaccurate marking of the fractions
Students who mark fractions in a very different position (several quadrants away) on the number line may need to address their understating that a fraction describes the relationship between the part and a whole (fractions as part-whole relationships) before trying to devise a system to compare or order fractions. If required, students could go back to partitioning and explore constructing the parts (unit fractions), combining these parts to make non-unit fractions that are between 0 and 1 (called proper fractions), and naming these new fractions (part-whole fractions). Encourage students to explore a range of many new fractions such as 3/7 , 5/8 , etc – even include some improper fractions.
Inaccurate marking of the fractions
Students who marked the fractions close but too inaccurately on the number line (in the next quadrant) may need to practise comparing two fractions (including non-unit fractions) before trying to order a number of them. For example, students could explain (using materials, diagrams or reasoning) how they know the larger of 2/3 and 3/4 , and then the larger of 2/5 and 1/4 . Marking five fractions on the number line involves being able to measure a fraction along the number line as well as comparing it to all the other fractions already marked. Appropriate drawing of fractions can help with comparing the size of fractions.
Inaccurate marking of improper fractions (5/4)
For students who correctly placed all simple fractions (other than 5/4), it is important to ensure that they do not develop the misconception that fractions are always between 0 and 1. Students could draw another number line and start to look at where other fractions such as 1/4 , 3/4 , are and build up to 5/4 ; or 1/2 , 2/2 , and 3/2 . Also look at the mixed fraction equivalent (e.g., 11/4and 11/2). Scaffold the students to construct these top heavy fractions by starting with the unit fraction of each and asking for non unit fractions with the same denominator. Try different fractions, 1/5 , 3/5 , 6/5 and even strange fractions such as 7/11 .

Accurately marking all fractions
For all students who accurately marked where the fractions go, ask them to explain how they know that is the correct location on the number line. Get them to justify how they know that the fraction is greater or less than adjacent fractions.
An extension of this resource could be to ask students to mark fractions on a number line between 0 and 2. This should ensure that students don't develop the misconception that all number lines (as well as all fractions) are between 0 and 1. Also explore the idea that fractions extend both ways along a number line, and can be between two other fractions. For number lines the whole tends to be "1" unless otherwise stated.
Numeracy resources
Book 7: Teaching Fractions, Decimals and Percentages, 2006:
- Fraction circles, (p.9), Advanced counting/early additive part-whole
- Trains (p.19) Early additive/Advanced additive/Early multiplicative.

