Two dice game III

Two dice game III

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Further Resources
This task is about comparing theoretical with experimental outcomes.
How to do the task
When two dice are thrown the numbers on top are added together. 
 dice-3-md-12-ii.png   Example: 2     +    3     =     5
 
a) i)
Do an experiment: throw the dice 36 times to try and find out which sums are more likely to come up.
Record your results in the table below. You may work in pairs for this part.
 
Sum of the two dice
Tally
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
 
 
 
ii)
 
Complete the frequency table below based on your actual results above.
 
 
 
 
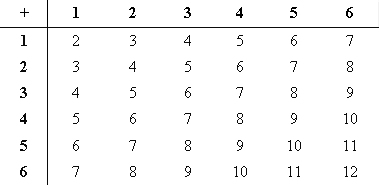
Answer the following questions by yourself.
 
The table below shows all the possible sums you can get when the numbers on the two dice are added together. 
 
                                      Number on Dice One:
 
 
b)
Using the information above, write in the table below how many times each sum occurs. These give the expected frequency for each number between 2 and 12. Two of them have been done for you (i.e., a sum of 2 occurs just 1 way and a sum of 11 occurs 2 ways).
 
 
 
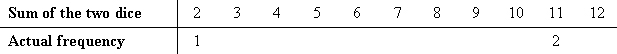c) Comment on the overall similarities or differences between the actual frequencies from your experiment in a), and the expected frequencies in the table in b) above.

 
 
 
 
 
 
 
d) Give two reasons why the actual frequencies in a) may be different from the expected frequencies in b).

  •  
     
     
     
  •  
     
     
     
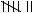Task administration: 
This task is completed with pencil and paper, and other equipment.

Equipment:

Two dice per student or pair of students.

Students may work in pairs for part a) only.

Level:
5
Curriculum info: 
Maths, Statistics, Probability
Key Competencies: 
Thinking, Using language, symbols, and texts
Keywords: 
probability, prediction, experiments, frequency tables
Description of task: 
Students throw two dice, add the numbers together, construct a tally chart of results, and compare theoretical with observed outcome.
Curriculum Links: 
This resource can be used to help to identify students' understanding of predicting the results of a chance situation, and checking consistency between experimental and theoretical results (including models of all possible outcomes).
 
Key competencies
This resource involves predicting the outcome of a probability situation, and communicating the findings of the probability experiment, and explaining variation. These relate to the Key Competencies: Thinking, and Using language, symbols and text.
For more information see http://nzcurriculum.tki.org.nz/Key-competencies
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Interpreting statistical and chance situations, set 5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
a)
i)
ii)
Systematic tallying of results (e.g., using ).
All frequencies consistent with tally chart.
b)  
Frequency table completed, as shown below.
 
Sum  2    3    4    5    6    7    8    9  10  11  12
Frequency  1    2    3    4    5    6    5    4    3    2    1

NOTE: Frequencies in bold were given
c)  
An overall statement given, e.g., "The two are very similar". 
 
Some specific comparisons made, e.g., "They were the same for 2, 4, 5, and 10, but different for the rest".
d)   Any 2 of:

  • The theoretical distribution rarely follows the experimental (everyday life) because of random variation in the experiment, e.g., "The differences are just luck," or "Everyone gets slightly different actual results".
  • One or more of the dice may be biased (unfair).
  • The dice may not be thrown fairly.

NOTE: Accept "Not enough trials conducted," or "Too small a sample size". (See comment below.)

NOTE: As the sample size gets bigger the expected frequencies get relatively closer to the actual frequencies. However, the probability of the actual frequency being exactly equal to the expected frequencies is higher for smaller sample sizes.