Using doubling and halving II
|
|
A doubling and halving strategy can be used to make some equations easier to solve.
|
a)
|
Use doubling and halving to write an easier equation to solve 3 × 14.
_____ × _____ = |
|
|
b)
|
Use doubling and halving to write an easier equation to solve 18 × 4.
_____ × _____ = |
|
|
c)
|
Use doubling and halving to write an easier equation to solve 36 × 5.
_____ × _____ = |
|
| d) |
Awhina needs to solve: 15 × 18 =
|
|
|
James needs to solve: 25 × 32 =
|
||
|
e) |
- Skip counting are is Stage 4: Advanced counting (in the multiplication and division domain).
- Repeated addition and the additive doubling are Stage 5 (Early additive part-whole) strategies.
- Doubling and halving is Stage 6: Early multiplicative part-whole.
- More sophisticated part-whole multiplication strategies are Stage 7: Advanced multiplicative part-whole or above.
| Y6 (11/2006) | ||
| a) | 6 × 7 = 42 [accept 7 × 6 = 42] | easy |
| b) | 36 × 2 = 72 [accept 2 × 36 = 42] or 9 × 8 = 72 [accept 8 × 9 = 42] | moderate |
| c) | 18 × 10 = 180 [accept 10 × 18 = 180] | moderate |
| d) |
270 and working using doubling and halving:
|
moderate moderate |
| e) |
800 and working using halving and doubling:
|
difficult moderate |
| Error | Likely calculation | Likely misconception | |
|
d)
e) |
140
610 |
15×18 = 10×10+5×8 = 100+40 25×32 = 20×30+5×2 = 600+10 |
Multiplication error – missing out factors Students expand (a+b)×(c+d) = a×c + b×d, but miss out a×d + b×c. Students only multiply the parts with the same place value together, i.e., multiply the tens and multiply the ones. Averaged over d) and e) about 10% of students made this error. |
|
d)
e) |
120
70 |
15×18 = 10×8 + 5×8 = 80+40 25×32 = 20×3 + 5×2 = 60+10 |
Multiplication error – missing out factors Students miss out some factors when multiplying two digit numbers. This is similar to the misconception above but the factors missed out can vary. |
|
d)
e) |
60 113 60 |
15×18 = 10+10 + 5×8 15×18 = 10×10 + 5+8 25×32 = 20+30 + 5×2 |
Substituting addition for multiplication Students use addition for some numbers instead of multiplication. |
|
d)
e) |
33
57 |
15×18 = 10+10 + 5+8 25×32 = 20+30 + 5+2 |
Students use addition for all numbers instead of multiplication. |
Students who used another strategy to solve the multiplication problem (correct or incorrect solution) should be encouraged to show how they could use doubling and halving to find their solution. These students could either be using a sophisticated advanced multiplicative strategy (stage 7), or a visual or additive strategy. The numbers have been selected to make the doubling and halving strategy an effective way to solve the problems.
Multiplication error – missing out factors or substituting addition for multiplication
Although this resource is primarily concerned with students being able to use a doubling and halving strategy. Students who misapplied rules for adding and multiplying will additionally need to develop their understanding about other multiplication strategies. They may need to use drawings or diagrams to help show how they solve double digit multiplication problems, and explain their reasoning for their strategy, students could look at how addition and multiplication relate through skip counting, repeated addition and then recognising the count of groups as a multiplication relationship, and then build up to double-digit multiplication problems to elicit their understanding of related place value issues. Students can also use an area graph to represent the multiplication relationship.
For example, for 25 × 32 the graph may look like:
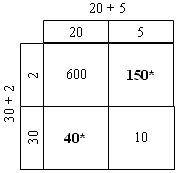
…and the answer can be found by totalling the components [20×30 + 30×5 + 2×20 + 5×2 = 600 + 150 + 40 + 10] This visual tool can help students recognise what part of the multiplication relationship they are missing out. The bolded numbers* represent commonly missed out numbers in two (or more) digit multiplication. This tool also scaffolds the two- dimensional array nature of multiplication. This relates to the cross products or to the vertical algorithm approach to multiplication (see Book 6: Teaching Multiplication and Division, pp.67-70).
Additive strategies
Students who used visual or additive strategies (e.g., skip counting and repeated addition) need to begin looking at developing multiplicative strategies. Some students doubled by adding. Doubling could also be regarded as one of the most basic multiplication operations. Students could be encouraged to recognise that adding a number to itself is "2 lots of that number", and that this is true for any number, i.e., the count of repeated additions is how many lots (factor) of that number. Exploring the link between repeated addition and multiplication, and basic doubling of numbers could support them starting to use multiplication.
Effectively using a doubling and halving strategy
Students who could apply doubling and halving efficiently could look at the other multiplicative inverse relationships and see if they can apply and generalise those, e.g., tripling and thirding (3×27 = 9×9). Students should also look at a wider range of multiplicative strategies and discuss which are more efficient and explain their reasoning.
The strategies students use can indicate their level of numeracy understanding. Students using skip counting are likely to be at Stage 4: Advanced counting (in the multiplication and division domain). Repeated addition and the additive doubling are Stage 5 (Early additive part-whole) strategies. Students who used doubling and halving are operating at Stage 6: Early multiplicative part-whole.
Some students used quite sophisticated part-whole multiplication strategies that may place them at Stage 7: Advanced multiplicative part-whole. Being able to use a variety of strategies is what indicates a student's understanding to move from early to advanced understanding of either additive or multiplicative stages.




