After-school training

At Te Kura o Manuiti 32 of the children play sports after school. Some children play just soccer, some play just basketball, and some play both soccer and basketball.
Twelve children attend both soccer and basketball. The total number of children taking basketball is 18. Show your answers for a) and b) in the spaces provided in the Venn diagram below.
a) Fill in how many children play basketball but not soccer.
b) Fill in how many children play soccer but not basketball.
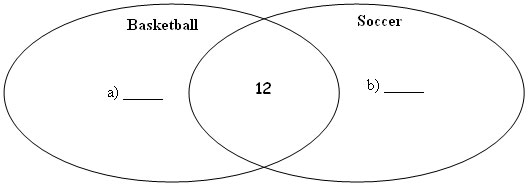
c) How many children in total play soccer? __________
| Y6 (11/2007) | ||
| a) |
6 |
moderate |
| b) |
14 (assuming answer in a) is 6) |
difficult |
| c) |
26 |
very difficult |
|
All three answers: 6, 14, 26 |
very difficult | |
Ideally, to indicate understanding about how a Venn diagram works students need to correctly construct and interpret all parts of the diagram. Venn diagrams are used to compare and contrast groups of things. They are a useful tool for formative assessment because they:
- can be used to generate discussion; and
- provide teachers with information about students' thinking.
It is important that students have already explored the nature of Venn diagrams and understand how they overlap (intersection) and how one set can be exclusive of the other.
For example:
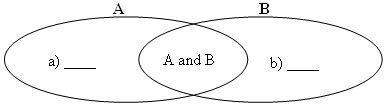
The value of a) will be the value of Set A not including the values of A and B, and b) will be the value of Set B not including the values of A and B (the intersection).
Recognising partial credit for conditionally correct student responses
Students who answered 18 [for a)] and 2 [for b)] indicate some awareness that there is overlap that needs to be adjusted for. They recognise that 32 – 18 = 14 but treat this answer as children playing soccer not playing soccer exclusively. They see that the intersection has 12, so to find the soccer only they subtract 12 from the 14 to get 2 for question b).
Almost a third of students used a correct strategy to work out question c). However some of these made an initial error which resulted in a different answer for c), but correctly indicated that the answer for c) is 12 more than the answer for b). For example many students who gave 14 as the answer for question c) are using a correct strategy to find the total soccer players, but using 2 [the incorrect number in question b)].
| Common error | Likely misconception | |
| a) | 18 |
Ignoring the effect of the intersection on the number playing just 1 sport Not understanding that the number playing just basketball is exclusive of those who also play soccer (B), i.e., the 12 students who play both are included in the 18 students that play basketball. |
| b) | 2 | Students aware that b) is exclusive of the intersection and that 32 – 18 = 14, but don't recognise that the 14 represents students who play only soccer. So subtract the 12 from 14. |
|
a) b) c) |
Various; e.g. 6 12 24 |
Ignoring that there are 32 students in total Does not ensure that the total number of students is 32, i.e. answer to a) + b) + 12 [intersection of a) and b)] = 32 |
|
a) b) |
10 10 |
Equates different subsets Assumes the number playing basketball only equals the number who play soccer only, but makes the total number of students equal to 32. |
| b) | b) = a) ≠ 10 |
Equates different subsets Assumes the number playing basketball only equals the number who play soccer only, but does not makes the total number of student equal to 32. |
| b) | 12 |
Ignoring the effect of the intersection on the number playing just 1 sport Assumes the number playing soccer only equals the number playing soccer and basketball (12). |
|
a) b) c) |
18 14 14 |
Completely ignoring the intersection of the sets Ignores the 12 students who play both sports, so deduces 18 + 14 = 32, and sees the 14 as representing all of those who play soccer. |
| c) | c) = b) |
Ignoring the effect of the intersection on the number playing just 1 sport Assumes the number playing soccer equals the number playing soccer only, i.e., not understanding that the number playing soccer equals the number who play soccer only plus those who play basketball and soccer. |
| b) | 6 | Mainly assuming the number playing basketball only equals the number who play soccer only – based on the correct answer to a). |
For students who did not identify the appropriate numbers to represent the aspects of intersection and exclusively basketball or exclusively soccer, developing Venn diagram for themselves should highlight the characteristics of the diagram. For example they could construct a Venn diagram for a logical situation that relates to themselves: students that have cats or dogs as pets (has dogs, has cats, has both, has none).
Developing the model – student role playing
Students may need to explore the concept by developing a model: The sets, Cats and Dogs, could be set up as two overlapping ovals on the classroom floor and the students stand where they think they should be. This would ensure that students can explore and discuss the meaning of
- having both cats and dogs;
- having only one;
- having neither;
and that the number of students is limited to the class size.
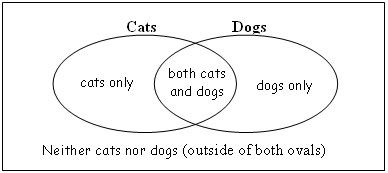
Students could explore visually what the parts of the Venn diagram mean using the language of total, only, both, not, and also intersection, and neither. Students could also explore the idea of one category and not the other (e.g., exclusively cats), – especially checking that the number of students does not add to more students than there are (checking the total).
Subtraction errors
For students who made subtraction errors, simply getting them to check over their work explaining what and why they subtracted amounts should eliminate the error. To further support students, use simple numbers to ensure that number knowledge is not a barrier for being able to use a Venn diagram.
Click on the link for further information about Venn diagrams as assessment resources.
Another website highlight features of Venn diagrams is: http://www.thoughtware.co.nz/pages/Venn.htm

