Cuisenaires and fractions

Cuisenaires and fractions

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about using Cuisenaire rods to work out fractions.
Use the Cuisenaire rods to help you answer the following questions. 
Hint: Place the Cuisenaire rods next to each other to find the fractions.
A diagram has been provided for the first question.
 
a) If orange is a whole then...   1 whole
 

i)

ii)

iii)

What fraction is yellow? _____

What fraction is white? _____

What fraction is red? _____
 
b)
 
 
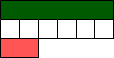
If the dark green rod is a whole then:
 
 
i)
 
ii)
 
iii)
 
What fraction is red? _____
 
What fraction is light green? _____
 
What fraction is yellow? _____
 
 
 
c)
 
If the dark green rod is \(1 \over 2\) then:
 
 
i)
 
ii)
 
iii)
 
What fraction is light green? _____
 
What fraction is red? _____
 
What fraction is blue? _____
 
d)
 
If the light green is \(1 \over 2\) then:
 
 
i)
 
ii)
 
iii)
What fraction is blue? _____
 
What fraction is red? _____
 
What fraction is dark green? _____
Task administration: 
This task is completed with pencil and paper, and other equipment.
 
Equipment: Students will need a set of the following Cuisenaire rods: 10 white, 5 red, 4 light green, and 2 each of yellow, brown, dark blue, brown, black, orange, magenta, and dark green
  • Creating Cuisenaire rods kits using snap lock bags may make the distribution and collection easier.
  • This resource is designed for students to work in pairs, or individually, if there are sufficient Cuisenaire rods.
  • The first question could be modelled by the teacher.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
fractions, cuisenaire rods, part-whole fractions, unitising, key competencies
Description of task: 
Students use cuisenaire rods to work out part-whole fraction problems.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 

a)

i)
ii)
iii)

1/2 or 5/10
1/10
1/5 or 2/10

b)

i)
ii)
iii)

1/3 or 2/6
1/2 or 3/6
5/6

c)

i)
ii)
iii)

1/4 or 3/12
1/6 or 2/12
3/4 or 9/12

d)

i)
ii)
iii)

3/2 or 11/2 or 9/6
1/3 or 2/6
1 (whole) or 2/2 or 6/6
Trialled in a classroom-based project about fractions, Y5 class, September 2005.
Teaching and learning: 
These questions involve part-whole understanding of fractions. Encourage students to verbalise the strategies they use to work out the answer. Often students can identify and share more than one way of getting to an answer.
This activity could be used in a journalling situation where students are asked to express their strategies and answers in writing.
 
Key Competencies: Thinking
This resource explores students' ability to think about part-whole fraction problems differently. Instead of being shown a whole shape with a shaded part and asked what fraction is shaded, students are given a shape and told what fractional value it represents. They are then asked to find another fractional part or the whole (referent whole). This requires them to use the information given to think dynamically about the relationships between the part and the whole rather than simply naming a shaded part from a given whole. This way of asking part-whole fraction questions challenges a learned "process" for solving such questions, and requires flexible thinking to make sense of the information given as the referent whole changes for each question.
Diagnostic and formative information: 
Questions c) and d), which named a rod as a half and asked students to work out what fractions the other rods stood for, were the hardest for students to solve. These questions challenge the convention used in many fraction questions, where students are asked to find the fraction of a whole (e.g., find  of 24).

Changing the way these questions are asked reduces the chance of students developing procedures without understanding.

Strategies
Students will often look for a unit fraction they can use as a base to build the other fractions, e.g.,

a) Orange is a whole and it takes 10 whites to make 1 orange, so each white is 1/10 , and red (which is 2 whites) must be 2/10 .
b) Dark green is a half (6 whites), so it takes 12 whites to make a whole (each white is 1/12). Light green is 3 whites (), and red is 2 whites which must be  .
c) Light green is a half, so it takes 6 whites to make a whole. This makes blue 9/6 , red 2/6 and dark green 6/6 .

Sometimes students will use a bigger block than white as the unit fraction, e.g., If dark green takes 3 reds to make a dark green, then it will take 6 reds to make a whole, so red is 1/6 .

  Common error Likely misconception
b) iii)
c) iii)		 1/5
1/3		 Students construct the fraction from the difference of the two rods:
b) the dark green and yellow rod;
c) the blue and the dark green rod.
c) iii) 9/10 Treats the half as a whole and thinks all fractions are less than 1
Students try to find what fraction the blue rod is of one green rod, and may not be aware that fractions can be larger than 1, so choose the largest fraction (closest to one) they know, i.e.,
c) i)-iii)
d) i)-iii)		 1/2 , 1/3 , 2/3
1/3 , 1/2 , 2/3		 Finds the smaller rod as a fraction of the larger.
Does not use the information in the stem of the question, instead uses the smaller rod as the part and the larger rod as the whole and finds the fraction accordingly, e.g.,

for c) dark green is two-thirds of blue, and d) red is two-thirds of light green, and

light green is half of dark green.

 

Next steps: 
For students who cannot work out the fraction of the given whole:

  1. Get students to show what rod is the whole and what rod is the part.
  2. Place the rods one over the other and ask "is it more than half?" "…more than 3-quarters?").
  3. Use the white rods to build up to the part and then to the whole (ask "How many white rods are there for the part? … the whole?").

1 dark green
6 white
1 red = 2/6 of dark green

 

  1. Once they are used to breaking down and building up using the white rods, encourage students toward using the other colours to work out the fractions. This way they will start to see a relationship directly between the different sized rods. One way of doing this could be by reducing the number of white rods to 5.

1 dark green
1 red = 1/3 of dark green
So 2/6 = 1/3 (equivalent fraction)

If students are unable to construct or name the fraction shown, they may need more experiences with simple partitioning of the Cuisenaires into pieces (white rods). They need to relate the number of pieces to the bottom number (denominator) of the fraction, name the unit fraction they are working with, and build up non-unit fractions (and name them) using these pieces. Try starting with the pink rod into 4 pieces, the light green rod into 3 pieces, and the yellow rod into 5 pieces.

  

For students who have difficulty when the cuisenaire rods are being compared to a half instead of a whole, encourage them to build up to what the whole would look like, lay the other rods for comparison over the "whole" and then apply whatever working strategy they were using earlier to find the fraction.