Fractional thinking concept map

Jonathan Fisher
 

Partitioning and Divided quantities

  

Fractions as part whole relationships
     

 Introduction

Fractional Thinking

Equivalence

Fractions as operators

  

Fractions and number lines

Unitising with fractions

  

Adding and subtracting fractions

* these categories are not separate, they can overlap significantly.

Component: 
Introduction

Underlying the development of fractional thinking is a number system that is different from the numbers that students have already had experience with.  Fractions have different rules for naming, quantifying, ordering, adding, subtracting, multiplying, dividing, etc.  Students will need to develop an understanding of these rules and be able to apply them when working with fractions.  Using a variety of visual and numerical representations for fractions can support students to build up experiences with the different areas of fractions (fractional constructs).

In the development of fraction knowledge there are important understandings and strategies that children develop as they learn about fractions.  For instance fractions can be:

  • about a relationship between a part and a whole (part-whole relationship); 
  • a result of a division (quotient)
  • compared and ordered (equivalence); and
  • like a function (operation) performed on a quantity.

These are some of the different constructs that fractions can take.  The order of the conceptual map clockwise from the introduction is a suggested order for instruction: Partitioning and divided quantities; part whole fractions; Equivalence (comparing fractions); Fractions and number lines; Fractions as operators; and Adding and subtracting  fractions.  The subsequent concepts tend to rely upon students having some understanding of the previous concepts.

The following pages introduce some of these important ideas, and provide links to related assessment resources.  The resources are designed to provide diagnostic and formative information about teaching and learning, to guide the development of the next learning steps toward developing a fuller understanding about the different constructs of fractions.

Resources

Partitioning and Divided quantities
What is partitioning?
Partitioning involves dividing an object or set of objects into parts. It can involve the breaking up of quantities into equal or non-equal parts. Partitioning into equal-sized (non-overlapping) parts is an important concept that lies at the heart of understanding fractions, percentages and decimals. The equal sharing of quantities (called partitive division) can also involve partitioning. Knowing that shapes, sets and quantities can be partitioned into equal-sized parts, and understanding the importance of equal-sized partitions is fundamental to recognising the part-whole relationship between the numerator and denominator in fractions.
When partitioning, it is important to use a variety of representations of sets, shapes and quantities to ensure that students are thinking and responding to different issues, not simply memorising images or procedures to solve problems. This helps students develop a more robust understanding of what a partition is.

Partitioning sets of objects (discrete)
The methods students use to partition a set of objects are as important as whether they can actually partition.  Some strategies are based on counting and matching.  Other strategies may indicate multiplicative understanding, such as: arranging objects into an array; finding the number of items per group by partitioning the set into a known number of equal-sized groups (partitive division); or finding the number of equal-sized groups given the number of items per group (quotitive division).

Using a counting strategy (partitive division)
Students who line the counters up and count out the counters into groups then count the number in each group are using a counting strategy. For example, if students knew they were sharing into three groups. Example:
Share 12 counters into 3 equally-sized groups.  
How many in each group?

This indicates that they understand the concept of equal-size and equal sharing with countable items (see equal sharing resources Equal sharing, Equal sharing II, Sharing counters, Equal sharing III).

Grouping strategy (quotitive division)
Students may line up the counters and indicate groups by circling pictures or grouping the counters (this lends itself more to quotitive division problems).  for example, if students knew they were sharing into groups of three. Example: How many groups can you share 12 counters amongst, so that there is 3 in each group?.  

Arrays
Students may arrange counters or draw pictures to illustrate an array.  This may help students visualise the groups that make up a set.  e.g., "If there are 12 counters and 3 equal-sized groups, what do we know about breaking 12 into 3 parts?"

Encouraging students to think about how to set out the counters to make breaking them into groups easier may promote the use of multiplicative strategies.  Start with small numbers divided into small groups, e.g., 6 counters into 2 groups, and then ask them to explain how they worked it out.

Recognising division in partitioning
If student are encouraged to describe what they have done with the numbers of the objects and groups in the set they could start to recognise the connection between partition and division.  For example ask how they could write what is happening as a number sentence.
Students that recognise the multiplicative relationship between the total and the number of groups, and are using a reverse multiplication (e.g., 6 × 3 = 18) or division (18 ÷ 6 = 3) strategy could try solving similar problems with larger numbers without using counters.   It is also important that students have experiences partitioning shapes.

Partitioning regions/shapes (continuous)
Students who have had limited experiences with fractions and partitioning may rely on the methods of cutting up they are familiar with.  If they have only ever divided up circles (pizza) they may think this is the only way to divide shapes up.  Using different shapes (such as squares or rectangles) which can be cut in many different ways or square pizzas can be used to challenge the students' concept of circular representations of fractions.  Hexagons, for example, can be easier to partition accurately into 3 or 6 equally-sized parts than circles. The number of partitions can relate to the shape to be partitioned.  Some shapes are more difficult to partition into different numbers, e.g., a square into 3 parts, a circle into 5 parts, etc. It is important that students build up many experiences of partitioning shapes starting with:

1. Halving of basic shapes, then halving, multiple times to derive other parts;
e.g.,
2. Partitioning a variety of shapes: squares, rectangles, circles, hexagons;
e.g.,
3. Partitioning shapes into a different number of pieces, e.g., 3, 5, 6, 7, 9, etc.

By partitioning shapes into an odd number of parts, and using a range of shapes, students develop a better understanding of partitioning.  This variety ensures that they are not only remembering partitions with certain shapes, but that they are developing a strategy to represent and understand fractions as a part of a whole.

Partitioning two shapes (or more)
Two shapes can be partitioned in a variety of ways.  Asking students to identify what each part is should promote rich discussion.  Students can be further probed by comparing the two questions "What fraction of both squares would each person get?" and then "How much of a (single) square would each person get?"

For example:
Show how to share these two cakes amongst 3 people.

Students may partition them in the following ways.
            Student 1                                         Student 2

Here Student 1 has used a bigger initial chunk than Student 2. Student 1 has realised that each person will get at least half of a cake and then examined what is left over. Research shows that students with more sophisticated understandings of fractions are more likely to use the biggest chunks possible when sharing.

Asking students to name the parts they have divided the shapes into:
Student 1: 1/2, 1/3 of a half (1/6);                             
Student 2: 1/3.

Asking how much of a shape each person gets:
Student 1: 1/2 and a 1/3 of 1/2 (1/2 +1/6);               
Student 2: 1/3 and 1/3 (2 lots of 1/3 = 2/3).

Then, ask how much of all the cake does each person get?
Student 1: 1/4 + 1/12;                                              
Student 2: 2/6 = 1/3.

NOTE: Student 1 needs understanding of how to add fractions and fractions as operators.

Students can discuss how the fractions are different, and why they may be different. By asking "what is the part?" and "what is the whole? (shape, set or quantity)" students can begin to explore the idea of relative thinking. 
Students should recognise that when the whole (also called the referent whole) is two squares the share is different than when it is one square.

For example, each person will get 1/3 of the two squares, or 2/3 of a square). 

Students' may also notice that the fraction is twice as big when the referent whole is half as much.

Key ideas about partitioning and divided quantities

  • Partitioning can involve dividing a number of objects into equal-sized groups (a discrete context); or
  • partitioning an object or shape into same-sized pieces (a continuous context).
  • Children with less developed partitioning skills will often not pay attention to the equal-size of their parts. • Students' experience with partitioning usually begins with partitioning sets of objects.  Generally students find this easier than partitioning shapes or quantities.  This is likely to be related to their experience with countable objects, where they can break sets into groups using a matching or counting strategy. • Partitioning usually begins with a repeated halving strategy that enables students to create fractions such as quarters or eighths.  The ability to create fractions that involve an odd number of parts, for instance thirds or fifths, develops later and requires practice
  
  • Different shapes can be more or less easy to partition.
    For instance, for many students it is more difficult to partition a circle into thirds than it is for a rectangle.
  • Students who are more mature in terms of understanding fractions are able to use larger size pieces or "chunks" when partitioning.
  
  • Activities involving partitioning should not be restricted to the early years.
  
  • Through partitioning, students can come to see that a fraction can be used to indicate the result of a division.  In mathematics terms this is called a quotient.  For instance 2/3 can be understood as meaning 2 objects divided into 3 equal parts. This is an important understanding of fractions.
  

Resources

Fractions as part-whole relationships

The concept of a fraction as a part-whole relationship is where one or more equal parts of a whole are compared with the total number of these parts that it takes to make up the whole. 
To understand fractions as part-whole relationships, students need to recognise the relationship between the bottom number (total number of equal-sized parts that make up the whole) and the top number (number of these parts of interest).  Understanding part-whole fractions can also involve:

sets of countable objects (discrete), 
shaded regions (continuous), and 
quantities (either continuous or discrete).

Most students' first introduction to fractions in the classroom as a part-whole comparison is with unit fractions, e.g., half, quarter, third (1/2, 1/4, and 1/3).  A unit fraction is one part of a whole.  That whole may be partitioned into many parts, but as long as it is only one of these parts of interest it is called a unit fraction.   For example if a shape is partitioned equally into n parts then each unit part is called one n-th which is written 1/n. Most fractions are non-unit fractions.  It is important to introduce simple non-unit fractions such as 2/3 and 3/4 at the same time as unit fractions to avoid students developing misunderstanding about all fractions from their limited experience with unit fractions.  Similarly, it is important to encourage students to explore fractions with different numbers such as 11/23, 9/13, etc,  improper fractions (e.g., 7/6, 4/3, etc), and mixed fractions 2 1/3, etc.

Fractional notation
Students beginning to understand fractions should be encouraged to use words to describe the parts, and delay the fractional notation until they have developed some understanding of what fractions represent. For all fractions, the notation convention is the bottom number (denominator) tells you how many equal parts make up the whole.  The top number (numerator) tells you how many of these parts are of interest.

Using part-whole understanding of fractions we can say the rectangle is one-fifth (1/5)

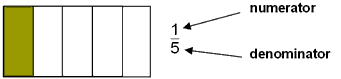
or shaded because there are five equal-sized parts and one of them is shaded.

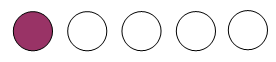
In the fraction "one-fifth", the one shaded part is described by the numerator and that four of these equal-sized parts make up the whole shape is described by the denominator. The equal-sized parts could be called "fifths". When solving part-whole fraction problems it is often helpful to remind students to ask themselves "What is the whole (shape or set)? and "What is the part (of the shape or set)?".

Fractions of shapes or regions (continuous)
A part-whole understanding of fractions involves identifying what fraction of a shape (or region) is shaded.  This context is usually continuous, when a part of the shape is shaded as below.   However if the shape has already been partitioned into equal parts it is essentially countable and therefore a discrete problem.

Example:
What fraction of this rectangle is shaded? Half - because there are two parts? Quarter - because four of those parts would make up the whole shape?

This problem is different from the 1/5 above because the pieces cannot simply be counted to construct a fraction.  Students here must use the shaded part and work out what fraction of the whole it represents (how many times the parts "goes into the whole").  They could be encouraged to draw lines to create equal-sized partitions to help them work out or explain their strategy.  Although some students may feel they are not supposed to draw lines on to the shapes, encouraging them to do so can help eliminate misunderstandings.
Asking students to explain or show their working can provide useful information about the strategies they use and their understanding behind their answer.  It is important to be aware of the strategies students employ to solve part-whole fraction problems and to ensure students are not developing a "narrow" solution method for solving without understanding the part-whole nature of fractions.

Unequal-sized pieces
Other similar questions, where the shapes are not evenly partitioned (as in the second shape below) can identify important misunderstandings. For example, what fraction of each of these shapes is shaded?

Another continuous context for fractions is distance or length.  Fractions can be shown on a number line.  This concept is explored further in Fractions and number lines.

Fractions of sets
Fractions can also represent relationships involving sets of countable objects (discrete).  Here the whole is considered to be the set and the part is the selection (or number) of countable items. For example:  What fraction of the counters is shaded?

 
Quantities
Part-whole fraction questions can involve identifying the fraction of a quantity. For example:
  • Bob has 5 marbles left from 15 at the start of the day. What fraction of marbles does he have left? For this question, the whole (referent whole) is 15 and the part is 5. So the part of the whole is 5/15. Students may recognise that there are three parts in the whole, which means the part is a third (1/3).

Context
Context can be important for students to begin to relate to their own experiences, but being aware of the meanings that underlie the contexts is important.  Circular pizzas are often used as a context for fractions, they tend to be cut into quarters and eights, but if students are asked a pizza question involving thirds or sixths they may find it difficult.  The context is meant to be realistic and one that students can relate to, and should therefore support the understanding rather than hinder it.
Students need to be introduced to a variety of shapes illustrating fractions as part-whole relationships - squares, rectangles, and hexagons are good starting shapes rather than using just circles.  This variety encourages students to use different strategies to solve the problems and develop their understanding about fractional representations rather than simply memorising common iconic fractions shapes without understanding:

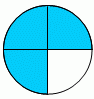
These may be well recognised as 1/3, 3/4 and 1/4 without understanding about the relationship between the part and the whole. Shapes like:

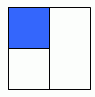
require students to begin developing an understanding about how much of the shape is actually shaded.


Finding the whole from a part
Part-whole fraction problems can also involve finding the whole when given a known part.  Asking fraction problems in this form ensures that students are not simply developing a formula for solving similar structured part-whole fraction questions (always finding the fraction of a whole).  An example of a resource that explores this is Cuisenaires and fractions. For example:

  • Bob has 5 marbles left. If this was 1/3 of how many he started with, how many marbles did he start with? The whole is unknown; The part is 5 and 5 is 1/3 of the whole.  So there are 3 of these parts in the whole, if each is 5 the whole is 15.

Example:

  •      If  is 1/3 draw what the whole would look like?
  •      If  is 1/4 what is ? ________.

It is important that students are asked questions in the form "what is the [whole] given the [part]" - not only "what is the [part] of the [whole]".  Otherwise they may develop only a limited understanding of fraction problems from having explored only simple part-whole problems.

Using the part to find another part
Students can also be asked fractions problems of the form:

  • If 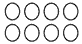is 2/3 what is 1/3? This problem can be solved by students finding (and/or drawing) 3/3and working out 1/3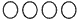 or by students recognising that 1/3 is half of 2/3, so the shape would be half the number of counters, e.g., 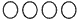or

or

  • If 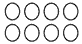is 2/3 what is 1/4? In this example, because the denominators are different (and one is not a multiple of the other), there is no immediate or obvious link between the 3 and the 4 except for recognising the common multiple of 12 and working with complicated calculations to solve the problem.  This problem can be solved more easily by students finding 3/3 then working out 1/4 of that, e.g., 3/3 is so 1/4 of that is


NOTE: Students would need to know that any fraction with the same number as denominator and numerator is one (a whole), e.g., 4/4, 3/3, etc.

Important ideas about part-whole fractions

  • The size of each part in a fraction must be equal.
  • The greater the number of parts needed to make a whole, the smaller each individual part is.  This means for instance, that 1/20 is smaller than 1/19.
  • Different fractions can be used to represent the same amount of a whole, depending on what size parts have been used.

Resources

Equivalence: comparing and ordering fractions

As students learn about fractions they come to understand them as a system of numbers. In particular, they realise that fractions have a size and can be compared, ordered, and represented as a point on the number line.

Strategies for comparing fractions
Students employ a range of strategies when comparing or attempting to compare the size of fractions. 

Drawing pictures
Students will often draw pictures to compare the size of fractions. These pictures can be useful to support or explain their understanding. However, they can sometimes be misleading, especially when the fractions are close together in size. 

Identifying fractions with the same denominator or numerator
Students will often use their part whole understandings of fractions to reason about fraction size. For instance, when a student understands that the size of the parts that make up a fraction depend on the size of the denominator, they can quickly see that fractions with the same denominator or numerator can be easily compared.

Unit fractions

Students can compare unit fractions by using their understanding of the meaning of the denominator. They can be aware that "the larger the denominator the smaller the fraction", because the whole is broken into more parts, therefore each must be smaller.

Fractions with the same numerator

Student comparing fractions with the same numerator is a derivation of comparing unit fractions.  For example, if one unit fraction is larger than another then any common count of the parts will be larger, e.g., 3/4 is larger than  3/7 because 1/4 is larger than 1/7, and there is the same number of parts being compared. 

Fractions with the same denominator

Students can compare fractions with the same denominator by comparing only the numerator.  This is almost no different from comparing whole numbers as the numerator is simply the count of units.  For instance, 5/7 is greater than 4/7, just because you have more of the same size part.  

Benchmarking fractions to well known fractions
Students will sometimes use a familiar fraction as a benchmark or reference point when comparing fractions.  For instance, they will note that 9/10 is greater than 7/8, as 9/10 is only 1/10 away from a whole, while 7/8 is 1/8 away. A half can be a useful benchmark.  Students often develop the understanding that a fraction is the same as 1/2 when the denominator is exactly twice the numerator.  They can use this relationship to place a fraction in relation to a half and then make comparisons with other fractions. For instance, 2/3 is greater than 1/2, while 5/11 is less than a 1/2.  This means 2/3 must be greater than 5/11. Some students who are able to identify when a fraction is greater or smaller than a half will not be able to tell you how close the fraction is to 1/2.  Asking how far away a fraction is from 1/2 can be a useful follow up question to encourage further understanding.

Using equivalent fractions
When comparing fractions, students will sometimes convert one or more of the fractions to an equivalent fraction with the same (common) denominator as the other fraction or fractions.  

For example,
Which fraction is larger 3/4 or 1/2?
Students may recognise that they can easily compare fractions if they both have the same denominator, and they may know that 2/4 is the same as (equivalent to) 1/2.  Using this knowledge of equivalent fractions they can compare 3/4 and 2/4.

Example,
Which fraction is larger 2/3 or 3/5?
Students may look for the lowest common multiple, in this case 15, and rename the fractions equivalent fractions, so the question becomes:

Which fraction is larger 10/15 or 9/15?

One common way to find equivalent fractions is work upwards from both fractions until a common denominator is found (trial and error)
Another way is to recognise the relationship between both denominators and have a sense of what the denominator needs to be.  Students then either extrapolate or cross multiply to work out what the numerator should be.

Some students will also convert fractions to equivalent decimals and percentages to make comparisons. Students use many methods to convert fractions to equivalent fractions or decimals and percentages including cross-multiplying.  These methods can often rely on learned processes that mask their true understanding of fraction size.

Misconceptions - Attempting to use whole number knowledge
Students will sometimes attempt to apply their knowledge of whole numbers to compare fractions. For instance, they will say 7/10 is greater than 4/5 as 7 is greater than 4. These students need to be challenged about the meaning of fractions. Using concrete materials can help them check their thinking.

Resources

Fractions and number lines

The ability to place a fraction on a number line follows from having a part-whole understanding of fractions, and being able to compare and order fractions.  The idea of fractions on a number line relates to the construct of fractions as measures. For some students using a number line can help them visualise the size of a fraction, and can provide them with a tool for representing and comparing fractions. 

There are two distinct types of resource about fractions and number lines:

  1. Writing or ordering fractions in pre positioned boxes along number line.  This can illustrate how a number line can be used to represent fractions of distance or length; or support the notion of a fraction being larger or smaller than another. For example:  Write the fractions that would go in the boxes below.

  1. Marking the fraction on an empty number line - this involves measurement and judgement of a fraction as a proportion of a length or distance.
    For example:  Show where 1/2, 2/3 and 3/4 would be on the number line below.

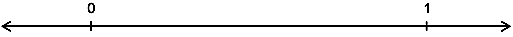
When using number lines it is also important to explore:

  • odd looking fractions (e.g., 9/15, 11/23, etc); and
  • number lines beyond 0-1 (e.g., 0-2, 1-3, 2-5, etc);
  • top heavy fractions (e.g., 4/3, 7/6, 12/5, etc); and
  • mixed fractions (e.g., 2 1/4, 4 2/3, etc).
 

For example: Show where 11/23 and 12/7 would be on the number line below.

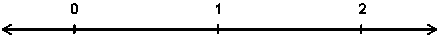
Context
The number line relates to the context of distance and length and questions like "how far along.?" can access student's prior understandings.  This context is already a part of student experience.  It can also be introduced using the context of a milk bottle, by asking how full is (a given mark) and using common fractional amounts used in conversation (i.e., a quarter, half, third, etc).

Resources

Adding and subtracting fractions

Adding and subtracting fractions is different from adding whole numbers.  Fractional parts can be added, but it is working out the value (or fractional name) of the sum that can be difficult.  For example, adding 1/2 +1/4 cannot be done by using rules for whole numbers, i.e., 1/2 +1/4 = (1+1)/(2+4) = 2/6 (or some derivation).  Adding fractional amounts involves working out some degree of common unit (denominator) before working out how many of these units there are (numerator).

Equivalent fractions
One strategy is if one fraction could be a factor of the other to use equivalent fractions, e.g., adding 1/3 and 1/6, 1/6 is a factor of 1/3 because there are 2 of them in 1/3. Therefore 2×1/6 is 1/3, so 2/6 = 1/3. So now there are common units (sixths) they can be added 2/6 + 1/6 = 3/6 (which is also a half).

This could also be done by using drawings

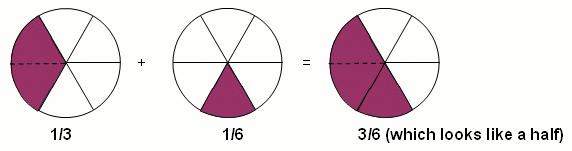
and in the array form:

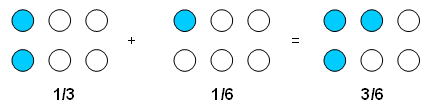
and for subtraction:

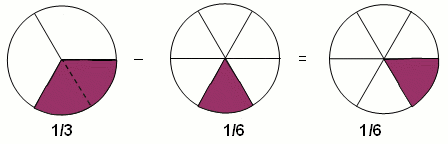
Equivalent fractions (common multiple)
One very common strategy is to find a common multiple, use that as the common denominator and then make appropriate adjustments to the top (numerator) by finding the fraction of the common denominator, cross multiplying.  This involves multiplying both the top and bottom number by the other multiple, and is based on the concept that multiplying top and bottom by a/a is the same as multiplying it by one (multiplicative identity), i.e., x × 1 = x

Example: Adding 3/4 + 2/3. Finding a common multiple of 4 and 3 - the most obvious and lowest is 12 3/4 (×3/3) + 2/3 (×4/4) = (3×3)/(4×3) + (2×4)/(3×4) = 9/12 + 8/12 = 17/12 (or 1and 5/12). Another way to adjust the numerator is by finding the equivalent fractional value of the new common denominator, i.e., asking "What is 3/4 of 12 (=9) and what is 2/3 of 12 (=8)?" This will result in 9/12 + 8/12 which can be solved as above.

Resources

Unitising with fractions

Unitising is about selecting a unit of measurement with which to measure or interpret other quantities. Unitising is a strategy that can be used to work out another quantity that relates to the unit selected. It involves the understanding of partitioning and equivalence of fractions to develop flexible thinking about fraction situations. This flexibility can in turn support further understanding about equivalence and fractions as rational numbers (in particular quotients – the result of division). Unitising can be defined as the assignment of a unit of measure to a given quantity or "chunks" that make up a given quantity (Lamon, 2007).

For example shaded fraction diagram

The shaded part could represent 7 (circles), or 3 1/2 (columns), or 7/12 (of a dozen), 1 3/4 (bundles of 4), or 1 1/6 (bundles of 6 or rows) depending on what "chunk" or unit you use as your reference whole or unit. All the answers above can be argued as correct and for each the unit (or chunk) is different.

How many shaded

Chunk

7

7/1

circles

3 1/2

7/2

columns

7/12

7/12

dozens

1 3/4

7/4

bundles of 4

1 1/6

7/6

bundles of 6 or rows

Another example could be the unit of measurement for a case of 36 soft drinks. The unit could be the case, a dozen, six-pack, or the individual bottles. Depending on what unit of measure is selected, the overall quantity of that measure can be different.

Questions that involve unitising require students to identify (or decide) the unit of measurement, and use this to explore how many of those make up the total. They can be Number and Algebra fraction type problems (e.g., Cuisenaires and fractions, Parts and wholes) or Measurement type problems involving repeated units (see Five dolls, Five swimmers).

Click on the link to read more about Unitising and re-unitising of fractions.

Resources

Fractions as Operators

Fractions as operators is about fraction as relational functions. A fraction acts as an operator when it is applied to a shape, set or quantity and the result is some form of derivative of that shape, set or quantity. For example, finding a fraction of a quantity is like applying a function to that quantity. 

Finding fractions of quantities 
For example, finding a fraction of a quantity is like applying a function to that quantity. The operation can shrink or enlarge the quantity to a new value. For example, finding 2/3 of a number can be the function where the operation is

  • "multiplied by 2 and then divided by 3";
  • "divided by 3 and then multiplied by 2"; or
  • other forms of a function.

Example: What is 2/3 of 12? This could be solved in a variety of ways: visually, or numerically. A range of solutions could be:

1) 2 × 12 = 24 and then 24 ÷ 3 = 8.
2) 2 × 12 = 24 and then 12 ÷ 3 = 4 and then 4 × 2 = 8
3) 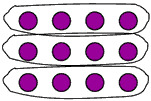(divided by 3) and then two of these partitions (multiplied by 2)
4) Finding 1/3 of 12 (=4) and then finding 4 + 4 = 8 (1/3 + 1/3 = 2/3)

Students indicate understanding of fractions as operators when they can identify different ways to apply and recognise the fraction as "one operation".  Fraction problems that involve fractions as operators are a common type of fraction question and often take the form: Find the [fraction] of a [shape/ set /quantity].

Examples of some fraction operation problems:

  • Find 3/4 of this shape
  • What is 7/8 of 56?
  • What is 5/6 of this set?
Promotional Text: 
Jonathan Fisher, 2006