Index arithmetic

Index arithmetic

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
 
Here are some numbers written in index form.
Simplify each of the following and write as single powers. 
Do not calculate the answer. Example: 5 × 5 = 52 
 
a) 83 × 84
 
 = __________
 
b) 56 × 5–3
 
 = __________
 
c) 28 ÷ 23
 
 = __________
 
d) 96 ÷ 98

 = __________
 
e) (75)3
 
 = __________
 
f)
 = __________
 
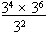g)
 
 = __________
 
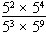h) 63 × 36

 = __________
Task administration: 
This task is completed with pencil and paper only.
Level:
5
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Keywords: 
index form, indices, powers, multiplication, division
Description of task: 
Students evaluate a number of expressions involving the laws of indices.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 8-9
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 

 

Y10 (03/2004)
a) 87 easy
b) 53 moderate
c) 25 difficult
d) 9⁻2 difficult
e) 715 difficult
f) 38 difficult
g) 5⁻6 difficult
h) 65 difficult

 

Results based on a trial of 169 students at Year 10 in March 2004.

Diagnostic and formative information: 
Likely misconception Examples
Does an exact calculation (more rare when negative indices are involved). a) 2 097 152
Adds indices instead of subtracting them. b) 59 = 56+3
Adds indices instead of multiplying them. e) 78 = 75+3
Multiplies base numbers (often with an incorrect index number as well). a) 647 = (8 × 8)4+3
Divides base numbers (often with an incorrect index number as well). c) 15 = (2 ÷ 2)8-3
g) 1–6 = (5 ÷ 5)6-12
Ignores the negative part of the index number. d) 92 = 98-6
Adds base numbers. h) 423 = (6 + 36)3
Wrongly evaluates 36 as 6 6. h) 69 = 66 × 63

 NOTE: More than one of these errors can often occur together, e.g., a) 6412 = (8 × 8)4× 3.

For a similar resource on laws of indices where students explain their answers see Student solutions.