Machine rules II

Machine rules II

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about working out the rules for some number machines.
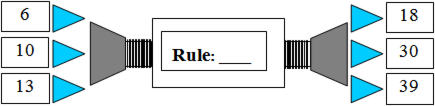
illustration: number machine
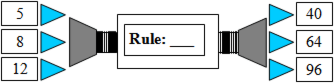
Numbers are put into machines and come out changed. Each machine uses a different rule to change the numbers.
 
Work out the rule for the machines below and write it for each machine. The first one has been done for you.
 
a)        
IN MACHINE 1 OUT
example number machine with rule multiplied by 8
 
 
 
b)        
IN MACHINE 2 OUT

number machine
 
 
Some machines have two rules that change the numbers. 
Work out the two rules for the machines below and write them for each machine.
 
c)        
IN MACHINE 3 OUT
number machine
 
 
 
d)        
IN MACHINE 4 OUT

number machine
Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Patterns and relationships
Keywords: 
rules, addition, multiplication, number patterns
Description of task: 
Students use given numbers to work out rules for number machines.
Curriculum Links: 
 
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Patterns and relationships, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
 

Y4 (06/2009)

b)

× 3

difficult
c) + 4
+ 10

both + 4 and + 10
 difficult
difficult
very difficult

d)

 ×2
+ 5

both × 2 and + 5

very difficult
very difficult
very difficult
Based on a representative sample of 158 students.
Teaching and learning: 
This resource explores students' ability to find a rule that "describes" patterns or relationships between numbers. This type of question requires students to identify a rule that will work for any of the numbers being inputted into the number machine. Additionally, the second two questions explore students understanding of how two operations can be combined to make a rule. These questions involve students drawing on a range of maths ideas: basic facts, patterns, relationships and generalisable rules.

Prior knowledge

  • Students really need to have an understanding about how a number machine works – numbers go in and are changed by a rule and come out after that rule has been applied to them.
  • Students would need to have a sufficient grasp of basic facts to make this resource accessible (e.g., 2- and 3-times table, see the Basic Facts concept map).
Diagnostic and formative information: 

One-quarter of students inserted numbers that were evident on the input/output lists. Many of these may not know how a machine works.

  Common error Likely misconception
b)
c)  i)
     ii)
d)  i)
     ii)		 6 or 10
5
9, 16, 19 or 26
4 or 10
8, 20 or 25		 Does not know how a number machine works
Students do not now how a machine works and insert numbers from the input/output lists – sometimes putting the operation sign in front of the number.
b) × 2, × 4 Basic facts errors
Students may have made basic facts errors.
b)
c) i)
    ii)
d) i)
    ii)		 3
4
10
2
5		 Not completely written with correct operator signs
Students have written the numbers, but not the correct operator in front of the number – this may also link to not understanding how a rule works.
b)
d)		 +12
+4 and +10		 Does not find a complete rule for both input numbers
Students find a rule that works for the top numbers, but not the numbers below.  This misconception relates to the fact that rules should to be generalisable to all numbers in the set.

NOTE: * students may also have put × or + in front of these

Next steps: 
Does not know how a number machine works
Students who did not know how these number machines work could explore simple one-part number machines (Machine rules) or arithmetic relationship maps (Addition rules or Multiplication rules).
 
Basic fact errors
Students who indicated basic facts errors may simply need to check their work, or may need to explore number machine problems within their basic facts ability.
 
Not completely written with correct operator signs.
Students who omit the operator required for the rule, need to be aware of the importance of providing a complete answer (for another person to read) as a part of successful communication of mathematical ideas.  The use of the ‘number machines’ supports students to write a general rule for the machine - this could then be used to illustrate how a general rule could also be found for other number patterns or sequences.

Does not find a complete rule for both input numbers.
Students who could not find a rule that worked for all numbers may need to explore questions more like a) which still has the mid-point numbers to scaffold between the two parts of the rule.  For number machines the rule must work for all the numbers.  This is an important understanding to emphasise with students.  Students could also explore this idea of a rule by looking at simpler number machines (e.g., question a) and discussing whether the rule +35 would be an appropriate answer, then working up to understanding that the rule must apply to all the numbers on the left for it to be valid.

 

Figure It Out: