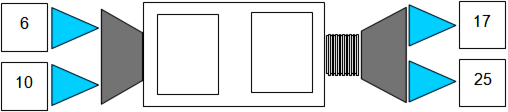
Machines with rules

Machines with rules

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about working out rules for some number machines.
illustration: number machine

  

Numbers get put into a machine and get changed by a rule. There are two parts to each rule.  Each machine has a different rule.
 
For the questions below write in the missing parts of the rule for the machine. The two parts of the first machine have been done for you.

  
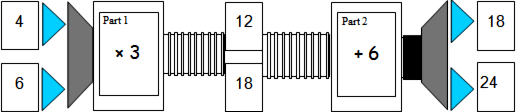
Example of number machine with rules times 3 and plus 4

Use the numbers to write the two parts of the rule inside the machine.


a)
 
The machine below has two parts to its rule. 
Use the numbers to write the two parts of the rule inside the machine.

b)
Part 1                   Part 2         

 

Task administration: 
This task is completed with pencil and paper only.
Level:
3
Curriculum info: 
Maths, Number and Algebra, Patterns and relationships
Keywords: 
number machines, functional rules, number patterns, addition, multiplication
Description of task: 
Students use given numbers to work out rules.
Curriculum Links: 
 
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Patterns and relationships, sets 4-5
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y6 (06/2009)
a)

× 3 + 4

 moderate
b)

× 2 + 5

 difficult
Based on a representative sample of 189 students.
Teaching and learning: 
This resource explores students understanding of how two operations can be combined to make a rule. The first example of the machine shows students how the machines work.

  • The first question (a) shows the two parts of the rule for the machine and the number in the middle.  This makes it notably easier to identify the two parts of the rule.
  • The second question (b) is harder because the middle numbers are missing: students have to work out both parts of the rule at the same time.  This relates to the idea of recognising two operations of a function.

Prior knowledge
Student really need to have an understanding about how a number machine works – numbers go in and are changed by a rule and come out after that rule has been applied to them.

Diagnostic and formative information: 

Many of the errors for both questions were basic facts errors.  These were answers that were close but just off a correct solution. There were also a number of students (about 10%) who indicated they did not know how a number machine worked (either did not answer the question or showed other working: finding sums, differences, cross products, etc.).

  Common error Likely misconception
a)
b)


b)

 +2 +6
+4 +8
+11 +15 or +11 +15
(two one-part rules)
16 & 42
(written in boxes)		 Does not know how a number machine works
Student does not know how a number machine works, and instead of moving through the machine (left to right) they find the relationship between the input numbers (e.g., for question a) looking at difference of 7 and 9 (2), and 25 and 31 (6)). Wrote a rule for each in each box – first box for the first number, second box for the second. Puts the sum of the two input numbers in the first box and the sum of the output numbers in the second box.
a)
b)		 3 and (+)4
2, 5 or
×2, 5		 Not completely written with correct operator signs.
b) ×1 +11 or ×3 – 1 or
+5 +6


+9 +6 or +10 +5

×3 –5

 Does not find a rule that works for both input numbers.
Students identify a rule that works for the first input number, but not the second.

Finds a rule that works for the second input number, but not the first. Students found a rule for the first input number and a different rule for the second – but not one rule for both.
Next steps: 
Does not know how a number machine works
Students who did not know how these number machines work explore simple arithmetic relationship maps (Machine rules) or arithmetic relationship maps (Addition rules or Multiplication rules), and then one-part number machines (Machine rules).

Basic fact errors
Students who indicated basic facts errors may simply need to check their work, or may need to explore number machine problems within their basic facts ability.

Not completely written with correct operator signs.

Students who did not write a complete rule with the operation signs need to be aware of the importance of providing a complete answer (for another person to read) as a part of successful communication of mathematical ideas.

Does not find a complete rule only for both input numbers.
Students who could not find a rule that worked for all numbers may need to explore questions more like a) which still has the mid-point numbers to scaffold between the two parts of the rule.  For number machines the rule must work for all the numbers.  This is an important understanding to emphasise with students.  Students could also explore this idea of functional rule through spatial and number patterns. For example students could discuss the relationship between the number of sticks to make a shape and the shape number (functional rule) in Making stick patterns or Matchstick patterns.

Figure It Out: