Travel posters

Travel posters

Pencil and paper
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about working out a missing dimension of a rectangular shape.
[not drawn to scale]
a)
The bigger photo has been enlarged from the smaller photo. Show how to find the missing dimension (x).
 

  

 

 

  
 
The length of x is __________ cm  
 
 
[not drawn to scale]
 
b)
The bigger photo has been enlarged from the smaller photo. Show how to find the missing dimension (y).
 

 

 

 
 
 
The length of y is __________ cm  
Task administration: 
This task is completed with pencil and paper only.
Copyright: 
Image source: PhotoKete
Level:
5
Curriculum info: 
Maths, Number and Algebra, Number Strategies
Key Competencies: 
Using language, symbols, and texts
Keywords: 
ratios, enlargement, scale factor, work samples
Description of task: 
Students work out the missing dimension on a rectangle and show how they obtained it using proportional reasoning.
Curriculum Links: 
Key competencies
This resource involves recording the strategies students use to solve problems involving ratios. This relates to the Key Competency: Using language, symbols and text.
Learning Progression Frameworks
This resource can provide evidence of learning associated with
Multiplicative thinking, sets 8-9
within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.
Answers/responses: 
  Y10 (11/2009)
a) 20
Describes any 1 of the following strategies:

  • Uses the factor of enlargement (or reduction) between the pictures.
    e.g., 16 ÷ 10 = 1.6; 32 ÷ 1.6 = 20 or
    10 ÷ 16 = 0.625; 32 × 0.625 = 20
  • Uses the ratio of the side lengths within a picture.
    e.g., 32 ÷ 16 = 2; 10 × 2 = 20  (doubling)
    16 ÷ 32 = 0.5 (or 1/2) 10 ÷ 0.5 = 20 (halving)
  • Cross multiples ratios of both pictures (either within or between pictures).
    e.g.,  x/10 = 32/16 [or 10/x = 16/32] so 16x = 320; x = 20 or
    x/32 = 10/16 [or 32/x = 16/10] so 16x = 320; x = 2
  • Uses a common proportionate amount of increase.
    e.g., 16 + 16 = 32 so 10 + 10 = 20
  • Other correct strategies.

easy
moderate
b) 15
Describes any 1 of the following strategies:

  • Uses the factor of enlargement (or reduction) between the pictures.
    e.g., 20 ÷  8 = 2.5; 2.5 × 6 = 15 or
    8 ÷ 20 = 0.4; 6 ÷ 0.4 = 15
  • Uses the ratio of the side lengths within a picture.
    e.g., 8 ÷ 6 = 1.3333; 20 ÷ 1.333 = 15 or
    6/8 = 0.75 (or 3/4) then 20 × 0.75 = 15  (or 3/4 of 20 = 15)
  • Cross multiples ratios of both pictures (either within or between pictures).
    e.g.,  6/8 = y/20 [or 8/6 = 20/y] so 8y =120; y = 120/8 or
    6/y = 8/20 [or y/6 = 20/8] so 8y =120; y = 120/8
  • Other correct strategies

moderate
moderate
Based on a representative sample of 144 students.

NOTE: Many students use fractional notation (16/32 etc.). We have accepted any explanations with fractions in them. More correctly the relationships are part to part and should therefore be expressed as ratios (16:32) or equivalent ratios (16:32 = 10:x). Students who express their working in ratios are working at the end of curriculum level 5.

 
Teaching and learning: 
  Common error Likely calculation Likely misconception
a)

b)

 26

18

 10 + 6 = 16 so 26 + 6 = 32
(or 32–16 = 16; 10+16=26)
8 + 12 = 20 so 6 + 12 = 18
(or 8 – 6=2; 20 – 2 = 18)		 Uses an additive relationship between side lengths
Uses the additive relationship between the side lengths rather than the multiplicative relationship. This was generally done by the absolute increase between pictures. The differences within pictures (the methods in parentheses) was rarely used

Student strategies
 
Students make comparisons in two different ways:

A. Comparing dimensions between pictures. This compares the respective sides of the two shapes (e.g., 16 ÷ 10 = 1.6 or 16/10 = 32/x).
B. Comparing dimensions within pictures. This compares the adjacent sides of the same shape (e.g., 32 ÷ 16 = 2 or 10/x = 32/16).

This was the case regardless of whether the strategies were correct or not.

Students used four different correct strategies:

  1.  Finding the scale factor between pictures and then multiplying (enlarging: 20 ÷ 8 = 2.5; 6 × 2.5 = 15), or dividing (reducing: 16 ÷ 10 = 1.6; 32 ÷1.6 = 20).
  2.  Finding the ratio (proportion) within a picture and then multiplying (32/16 = 2; 10 × 2 = 20).
  3.  Equating the ratios (proportions) of the pictures and then cross multiplying. This can be either between pictures (16/10 = 32/x) or within pictures (10/x = 32/16).
  4. Expressing the ratio (proportion) within a picture additively (16+16 = 32 so 10+10 = 20).

    

  • The most common strategy was finding the scale factor between pictures (A), especially for part b).
    In part a) the scale factor 16 ÷ 10 = 1.6 was far more commonly used than 10 ÷ 16 = 0.625
    In part b) scale factor 20 ÷ 8 = 2.5 was far more commonly used than 8 ÷ 20 = 0. 4
  • The second most common strategy was finding the proportion within a picture (B).
    In part a) the proportion 32/16 = 2 was far more commonly used than 16/32 = 0.5 (or 1/2).
    In part b) the proportion 6/8 = 0.75 (or 3/4) was far more commonly used than 8/6 = 1.33

Students using these two predominant strategies had higher mean abilities than those with other correct strategies. In particular, students who used equating proportions then cross multiplied, had lower mean abilities, indicating that they may be proceeding more procedurally than with understanding of the proportional relationship. Each of these strategies had very high success rates (see Summary of correct strategies). Apart from four students who used various other alternative methods, no other strategies led to correct answers.

Next steps: 
Uses an additive relationship between side lengths
Students need to see that enlargement works by multiplying each side of a shape (here a rectangle) by the same amount.

One way to get students to see that their additive strategy does not work is to get them to draw one of the shapes to scale (say the 16 by 32, but done in mm, not cm). They could then draw the 10 by 26 shape. Ask them to compare the two shapes. The latter looks longer and thinner. They could also draw smaller shapes that apply the same rule (e.g. 4 by 20). This is much thinner. Much bigger rectangles that use this rule get more and more like squares (e.g. 84 by 100, 984 by 1000). Simpler sets of rectangles (1 by 3; 2 by 4; 6 by 8; for example) may be used. Here the scale factors are whole numbers.

This can lead to a discussion of the length of one side relative to the other – "It is twice as long"; "It is two and a half times longer". These can be expressed as fractions (16/32) or, more correctly, as ratios.

If students are used to equivalent fractions, or equivalent ratios, utilise this. Ask "What is a fraction that is equivalent to 1/2 ?". They may well respond 2/4 , 3/6 and hopefully will see that 16/32 is also equivalent. Ask them then to give the fraction that is equivalent to ½ where the numerator is 10. They should respond with 10/20 . Relate these facts to the pictures.

For part b), the most relevant fraction equivalent to 6/8 is 3/4 . 12/16 and 18/24 are also equivalent (multiplying the numerator and denominator by 2 and 3 respectively) with 15/20 being sandwiched part way between. 15/20 can also be got by multiplying the numerator and denominator by 2.5 (= 20 ÷ 8).

Students who got correct answers
Get students to explore different ways that the problem could be solved (See Examples of student strategies). Get them to discuss and compare the relative strengths of different approaches, and to see the similarities and differences between them. They could also critique the incorrect strategies.

Other resources

For other ARB about ratios, use the keywords or click on the link; ratios AND NOT simplest ratio. Most of these are not involved with ratios between sides of similar rectangles.

For other ARB about enlargement and scale factors, use the keywords or click on the link; scale factors AND NOT invariant properties. Most of these involve using given scale factors rather than using scale factors to find missing dimensions.

Examples of student strategies – Correct Strategies

Finding the scale factor between pictures (Using scale factor > 1):

Part a) Using numerical statements only.


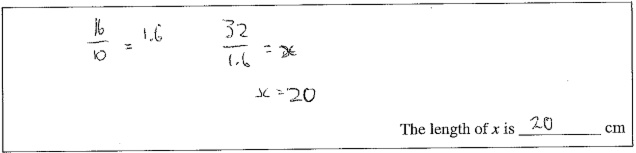
Part a) Using numerical statements plus a pronumeral.


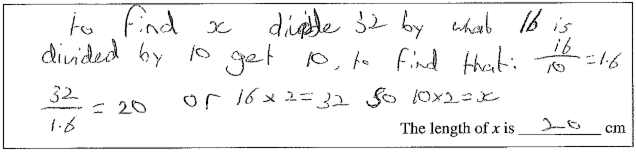
Part a) Using word and numerical statements plus a pronumeral.


Part a) Using numerical statements plus a pronumeral.

Equating the ratios (proportions) of the pictures and then cross multiplying within pictures:

Part a) Using numerical statements plus a pronumeral and using ratios.


Part a) Using numerical statements plus a pronumeral and using ratios.


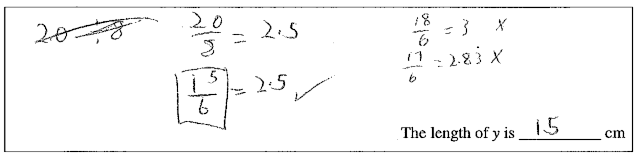
Part b) Using numerical statements, using fractions and using trial and error.

Finding the ratios (proportion) within a picture (Using proportion > 1):

Part a) Uses doubling on both pictures written only in words.


Part a) Uses doubling on both pictures with words and mathematical notation.


Part b) Using numerical statements. Includes the proportion <1, but uses the bigger one. Uses fractional notation.

Finding the ratio (proportion) within a picture (Using a proportion <1):


Part a). Uses halving on both pictures. Also uses a scale factor of 1.6

Expressing the proportions additively within a picture:


Part a). Expresses doubling as 16 + 16 instead of 2 × 16.

Other correct responses


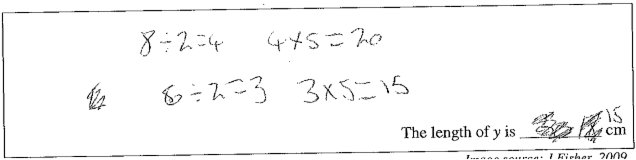
Part b). Takes a common factor of 2, then uses a common multiple of 5. Equivalent to a scale factor of 5/2 .


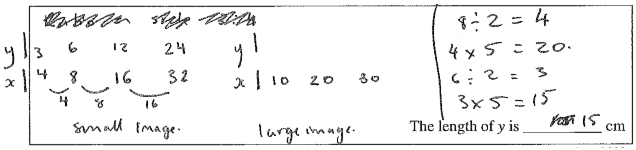
Part b). Draws a table but cannot complete for the large image. Takes a common factor of 2, then uses a common multiple of 5. Equivalent to a scale factor of 5/2 .

Examples of student strategies – Incorrect Strategies

Uses an additive relationship between side lengths between pictures:


Part a) Finds the difference between respective sides, and applies rule to other pair of sides.


Part b) Finds how much to add on to one side to get the respective side. Applies this rule to other pair of sides.


Part b) Finds how much one pair of dimension decreases. Decreases the other by the same absolute amount.