Using a quadrilateral key diagram
0
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about using a classification key to identify propoerties of shapes.
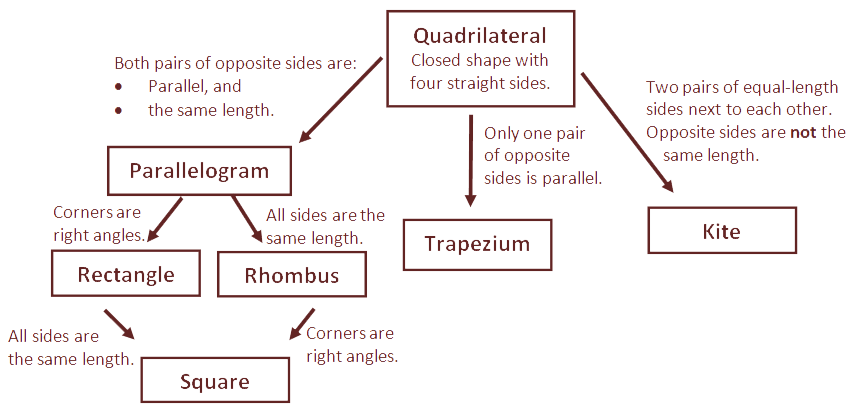
This diagram is called a classification key. It shows the properties that define a family of shapes.
Use the classification key to answer the following questions.
Task administration:
This task can be completed with pencil and paper or online (with SOME auto marking displayed to students).
Level:
4
Curriculum info:
Key Competencies:
Keywords:
Description of task:
Students use a quadrilateral key to answer questions about attributes of quadrilaterals.
Curriculum Links:
This resource can help to identify students' understanding of shape properties.
Learning Progression Frameworks
This resource can provide evidence of learning associated with within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.Answers/responses:
| Y7/8 (03/2017) | ||
| a) |
Parallelogram:
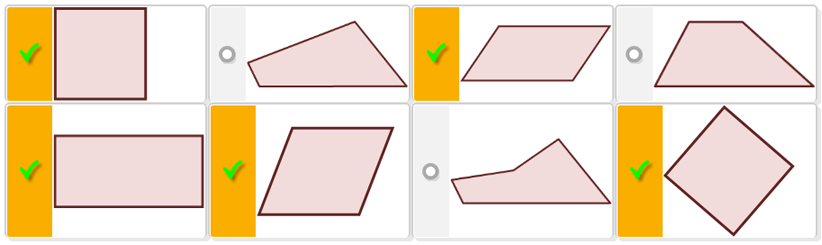
Any three properties of a parallelogram:
|
moderate
(all 5 shapes correct)
or
easy
(at least 3-4 shapes correct)
|
| b) |
Trapezium:
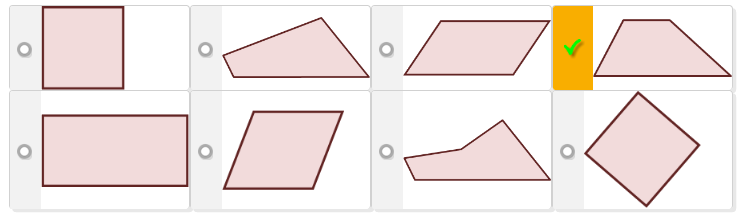
Any three properties of a trapezium:
|
moderate
(correctly identified with no other incorrect shapes identified)
or
easy
(correctly identified trapezium, but with 1 other incorrect shapes)
|
| c) |
Rhombus:
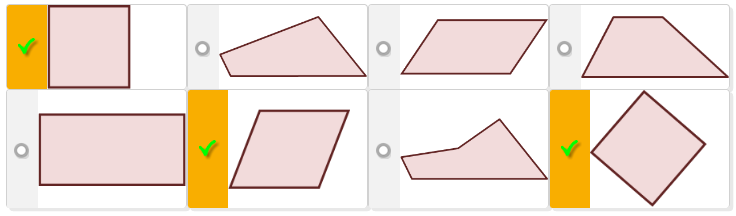
Any three properties of rhombus:
Note: some students identified
|
difficult
(all 3 shapes correct)
or
moderate
(at least 1-2 shapes correct)
|
Based on a sample of 40 Y7-8 students.
* these properties are true for all quadrilaterals.
Teaching and learning:
This task is about using shape properties to classify quadrilateral shapes on a key diagram. A critical aspect of this is to recognise the hierarchical relationships within the key diagram. Moving down the diagram the properties are shared for all shapes under that classification. For example, all parallelograms have both pairs opposite sides parallel and both pairs of opposite sides congruent, therefore all shapes under parallelograms in the diagram (rectangle, rhombus, square) will have these dependent properties.
Properties also help to distinguish between different shapes, e.g., a parallelogram with right angled corners is a rectangle (or square) and a parallelogram with all congruent sides is a rhombus.
Students should have some understanding about how to read a simple key diagram and how the relationships work down and across the diagram. This task could be used to further explore or consolidate that understanding with classification keys.
Diagnostic and formative information:
Question a) Parallelogram:
i) A number of students did not identify all five parallelograms.
ii) Statements that lack sufficient detail/not true for all parallelograms:
- has two obtuse angles and two acute angles (relying on visual information)
- sides can be on an angle (relying on visual information)
- corners are right angles (not true for all parallelograms)
- all sides are congruent (not true for all parallelograms)
- like a rectangle on an angle (relying on visual information).
Question b) Trapezium:
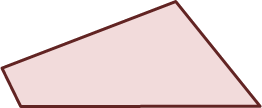 (no parallel sides) and
(no parallel sides) and 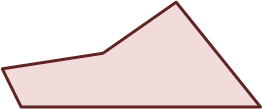 (not 4-sides)
(not 4-sides)
i) A number of students selected the following two shapes as a trapezium:
 (no parallel sides) and
(no parallel sides) and  (not 4-sides)
(not 4-sides)
Note: the first option is regarded as a trapezium in North America (defined: no parallel sides), but not elsewhere (defined: exactly one pair of opposite sides).
For further exploration of these contradictory definitions, see Trapezium [Wikipedia]
ii) Statements that lack sufficient detail/not true for all trapezia:
- one pair of opposite sides (insufficient detail)
- a set of opposite parallel lines (insufficient detail)
- no opposite sides can be congruent (incorrect for trapeziums)
- all sides can't be equal (not specific to trapezium, kite)
- long side at the bottom (relying on visual information)
-
sides are angled and not straight up and down (relying on visual information)
-
no sides can be parallel (incorrect - but true for US definition of "trapezium")
-
all sides are uneven (insufficient detail)
-
top and bottom line are different length (relying on visual information - but logical if only one pair of parallel lines)
-
two angled sides and two straight sides (relying on visual information)
-
has two obtuse angles and two acute angles (relying on visual information).
Question c) Rhombus:
i) A number of students selected the following two shapes as a rhombus:
 and
and 
ii) Statements that lack sufficient detail/not true for all rhombus:
- not parallel (incorrect)
- sides are on an angle (relying on visual information)
- corners are right angles (relying on visual information).
Across all three questions, students who identified more correct shapes also tended to use the information from the key to justify their selections. They also recognised that shapes having four sides and straight lines were also properties of all quadrilaterals.
Student misconceptions appeared to be based around three main ideas:
- Not reading the relationships from the quadrilateral key diagram correctly, i.e., not correctly applying the properties for shapes below in the diagram or the properties that distinguish between shapes.
- Identification of properties is not sufficiently detailed, e.g., for a trapezium some students noted it had to have one pair of parallel sides not specifying that it must be "only" or "exactly" one pair of parallel sides; or for the rhombus, all sides must be parallel, which lacks detail about which sides. If all sides were parallel the shape would be a pair of parallel lines (straight or not) or a donut shape.
-
Relying on a very strong dominant, pre-conceived image (sometimes called a visual prototype) for what a shape looks like. Rather than using the properties, students rely on whether the shape looks like the shape they remember. For example, they may think that a parallelogram only ever looks like a regular parallelogram
 . Similarly, a square is often portrayed
. Similarly, a square is often portrayed  not
not  (or at some other tilt angle). This is the result of the over-use of a single representation of a shape (pre-dominantly regular shapes) that reinforces students' ideas about what is (and is not) a particular shape.
(or at some other tilt angle). This is the result of the over-use of a single representation of a shape (pre-dominantly regular shapes) that reinforces students' ideas about what is (and is not) a particular shape.
Next steps:
Not correctly reading the quadrilateral key diagram
Students who incorrectly identified and did not attribute the correct properties to the shape may need to further explore how a classification key works, especially how all the properties are shared for all shapes below a given shape. Using the classification key they pick a shape from within the key and then, as they move down the key, list all the shape properties. They should look to include properties that come from polygons (straight sides, closed shape), quadrilaterals (4 sides), and then the more specific properties of the shape they have picked.
Students could also explore the use of classification keys in science. Science resources that explore keys are Using a metals key, Naming plants, Birds' egg detective (L3), and for further tasks using the key word classification keys or keys.
Relying on the visual representations of shapes rather than the shape properties
Students who incorrectly identified shapes and attributed properties based on how the shape looked need to focus on identifying and describing the properties of the shapes. They need to challenge their preconceptions about what a shape looks like. This could be done by presenting them with counter examples. The shapes in this task have been deliberately selected to challenge the visual prototypes that students may have formed, and to explore the actual properties of a number of shapes.
Students could also be asked to draw 5 each of different parallelograms, trapezia, and rhombuses to highlight that ther are many variations of each shape. These shapes could be shared with a buddy or a group by talking about how each of the shapes still meets the definitions of parallelogram, trapezium, and rhombus. Students could also be asked if there were anymore of these variations that could be drawn.
Another example of a student exploration could be Trapezium or not? (similar to the Square or not? Triangle or not? Rectangle or not? resources)
Which if the following is a trapezium and how do you know?













Students would need to think about all properties of a trapezium, i.e., properties that come from being polygons (straight sides, closed shape), quadrilateral (4 sides), and then the properties specific to a trapezium.
Not providing sufficient details or incorrect details
Students who did not provide sufficient descriptions or details of properties for the shapes could be asked to work with a buddy and either use their descriptions to guess which shape they were identifying, or play a guessing game with only yes or no answers (e.g., Does the shape have right angles?).
In addition, giving students the opportunity to develop definitions of shapes can also help to focus them on the shape properties which helps with describing the properties. The resources Triangle or not?, Square or not?, and Rectangle or not? provide examples that draw attention and explore the properties of these shapes. Also, to give students exposure to different sorts of shapes and construction of definitions (or clues), they could explore the resource, What Shape am I?
For further information about shape properties, see the Geometric Thinking Concept Map.

