Square or not?
0
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about identifying whether shapes are squares and what makes them squares.
Task administration:
This task can be completed with pencil and paper or online (with SOME auto marking).
Level:
3
Curriculum info:
Keywords:
Description of task:
Student select shapes that are similar but not squares and explain what makes them squares or not.
Curriculum Links:
This resource can help to identify students' understanding of shape properties with justification.
Learning Progression Frameworks
This resource can provide evidence of learning associated with within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.Answers/responses:
| Y6 (11/2015) | ||
| a) |
It is not a square
Sufficient explanation involves identifying the specific feature of the shape that makes it not a square, e.g., the shape is not closed, or does not have 4 corners/sides.
Examples of explanations
|
very easy |
| b) |
It is a square
Sufficient explanation involves identifying the specific feature/s of the shape that make/s it a square, e.g., the shape is closed, has 4 corners/sides, and all 4 corners/sides are equal.
|
easy |
| c) |
It is not a square
Sufficient explanation involves identifying the specific feature/s of the shape that make/s it not a square, e.g., the shape is not closed, or does not have 4 corners.
|
very easy |
| d) |
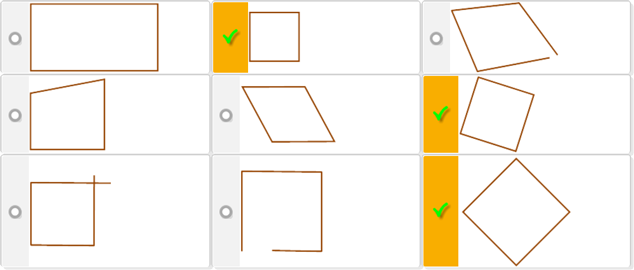 |
All 4 correct - moderate
First square - very easy
Tilted square - easy
Diamond square - moderate
|
| e) |
Explanation involves some combination of :
And does not include any incorrect additional rules such as must not be on an angle (tilte), etc.
Examples of explanations
NOTE: At this level it might be expected that sutdents provide 1-2 points of a definition.
|
|
NOTE: A shape only needs to lack one property to disprove that it is a square. However, to show that a shape is a square it should have all properties accounted for (e.g., sides, corners, equal sides, closed).
Teaching and learning:
This assessment resource encourages students to share their understanding about the properties of shapes. In particular, the shape properties that make up a square: a closed plane figure with four straight equal sides and four corners with equal/right angles.
Over-using of a single representation of a square can encourage students to develop a more limited sense of what is (and is not) a square. The shapes in this assessment resource have been deliberately selected to break open the visual protoype that students may have formed, and to explore the actual properties of squares.
Note: a square is a subset of rectangles, this is further explored in the assessment resource: Rectangle or not?
Diagnostic and formative information:
Some of the responses below are interesting because of the additional ideas they reveal about students' understanding of squares and shapes, in general.
For example
- It can't be a square because it's a diamond.
- The lines are even and it looks like an olden day tv
- Its a half of a rectangle has no gaps and can be rotated as a dimond
- It's a common shape it is easy to know
- It's a square, it's just tricking your mind to think its a diamond
Also notable was the lack of explicit equality of the (straight) sides/corners that is needed for the definition a square. There is still a sense of how a common square looks (like half of rectangle).
Next steps:
Not correctly identifying a square
Students who identified that question a) or question c) were squares may need to explore the properties and definition of a square. Students could be asked to work in groups to come up with a definition of a square. The examples of squares and 'not squares' from this assessment resource could be used to test their conjecture. In addition, the students' responses included in the Marking and Diagnostic information could be shared and discussed. Discussion will likely flow to open shapes, and what defines a corner and a side. These basic ideas might need further clarification. Students could be asked to locate a definition for a corner, and develop examples of what are corners and what are not. Similarly, students should explore the definition of a side, and be able to discuss this for shapes such as question c). Once they have more awareness about sides and corners they will be more able to determine the important properties for a definition. Ultimately, it is important to get students noticing and considering the properties of shapes, and using this to argue whether a shape is or is not a square, triangle, rectangle or other shape.
Incomplete definition
Students who gave brief and/or incomplete reasoning for question e) could explore the full definition of square. Using counter examples for any property that is not accounted for in their definition (e.g., if they don't include corners in the definition show a shape with 4 sides, but 3 corners (4 sided open shape), or an open almost square, and ask them what else might need to be added to the definition.
Further teacher, peer modelling, or sharing of sufficient definitions may also help supplement their understanding of what is needed in a definition. A definition for a square for further exploration could be:
- "A closed plane figure with four equal straight sides and four right angles."
- " A four sided polygon characterized by right angles and sides of equal length."
For further information about shape properties see the Geometric Thinking Concept Map.

