Dividing by three and five
0
Overview
Using this Resource
Connecting to the Curriculum
Marking Student Responses
Working with Students
Further Resources
This task is about identifying numbers that are divisible by three or five.
Task administration:
This task can be completed online (with SOME auto marking).
Level:
3
Curriculum info:
Key Competencies:
Keywords:
Description of task:
Students identify multiples of 5 and of 3, and explain their reasoning.
Curriculum Links:
This resource involves explaining rules for divisiblity. This relates to the Key Competencies: Thinking and Using language, symbols and text.
For more information see https://nzcurriculum.tki.org.nz/Key-competencies
Learning Progression Frameworks
This resource can provide evidence of learning associated with within the Mathematics Learning Progressions Frameworks.
Read more about the Learning Progressions Frameworks.Answers/responses:
| Y6 (04/2016) | ||
|
a)
|
Selects 25, 70, 105, 175, and 300
Students explanations that involve recognising that the ones are either five or zero:
|
very easy
(All 5 correct and none incorrect)
moderate
(correct explanation)
|
|
b)
|
Selects 33, 45, 96, 138 and 444
Student explanations that involve recognising that either the digits added together are divisble by 3 or some other appropriate rule:
|
very difficult
(All 5 correct and none incorrect)
difficult
(3 or more correct and none incorrect)
very difficult(correct explanation)
|
| c) |
 |
very difficult
|
Based on a sample of 69 Year 6 students.
Diagnostic and formative information:
Students found question a) quite easy, as counting in 5s starts at Level 1 of the NZ Curriculum, and has an easily recognisable pattern (ending in either a zero or 5). Students found it easy to identify and explain the pattern. For question b) students could easily identify the numbers divisible by 3 if the last digit of the number was also a factor of 3, but they were less sure for numbers such as 138 or 444. Students were easily able to see that 23, 76, and 313 were not divisible 3. However, overall question b) was very difficult.
| Common error | Likely misconception |
| b) not selecting 45, 138 or 444 |
Student does not know how to divide by 3 or
Student does not know the rule for divisibility by 3
|
|
b) Selects 23, 76 or 313
c) Selects 26 (as divisible by 3)
|
Students may think that if the last digit of a number is a factor of 3, then the number is also divisible by 3.
|
|
c) 45 or 75 (divisible by 5 only)
|
Students only look for a single solution and do not identify that these numbers are also divisible by 3. |
Next steps:
Student does not know how to divide by 3Students need to be encrouaged to see the part-whole nature of numbers to help them identify the larger number factors of 3. Students could then look at the larger numbers like 138 and break them down to obvious factors of 3, such as 120 and 18 which are easily identified as divisible by 3 (and therefore the whole number is divisible by 3 - distributive law [Wikipedia]). Similarly, students could break 444 into 300 and 144 which is in the 12 times table, so must be divisible by 3 (or they could break into 390 and 54, etc).
Student does not know the rule for divisiblity by 3There are divisibility rules for 3 (https://en.wikipedia.org/wiki/Divisibility_rule#Divisibility_by_3_or_9), but students should be given the chance to work out their own strategies for solving divisibility before this is explored. Students could then explore if and then why this rule works. Students could try a range of numbers that are or are not divisible by three. They could then make conjectures about what makes a number divisible by 3 (e.g., all the digits are divisible by 3). They could then test their conjectures on other numbers.
Students may think that if the last digit of a number is a factor of 3, then the number is also divisible by 3.
Students could test if their rule works by dividing 23, 76 or 313 by 3.
Students only look for a single solution
Sometimes drawing attention to all the categories available in this task (divisible by 5 only, 3 only, 5 and 3, and neither) and considering these ahead will help students to check other categories before making a decision. For example, once students have noted that the numbers are divisible by 5 they can then be asked if 3 is also a factor (i.e., are they divisible by both 3 and 5?).
To support the idea that numbers can be divisible by a range of factors, students could be asked about numbers like 6 (2 and 3) and 12 (2 and 3 and 4), and 20 (2 and 4 and 5) and be asked to identify all the different factors. They could also mark or colour in a hundreds board to see the overlap as well as the patterns that develop.e.g., multiples of 3 6 and 9 are coloured in the representation below.
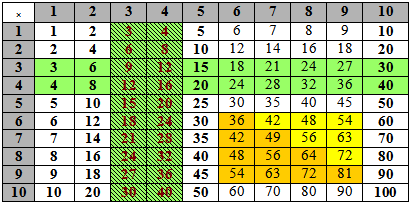
See the Basic facts conceptual map to explore the patterns for factors in Multiplication.
See the Basic facts conceptual map to explore the patterns for factors in Multiplication.
Divisibility rules for 3 and 9 on Wikipedia
Also for some background viewing about divisibility, see the Khan Academy

